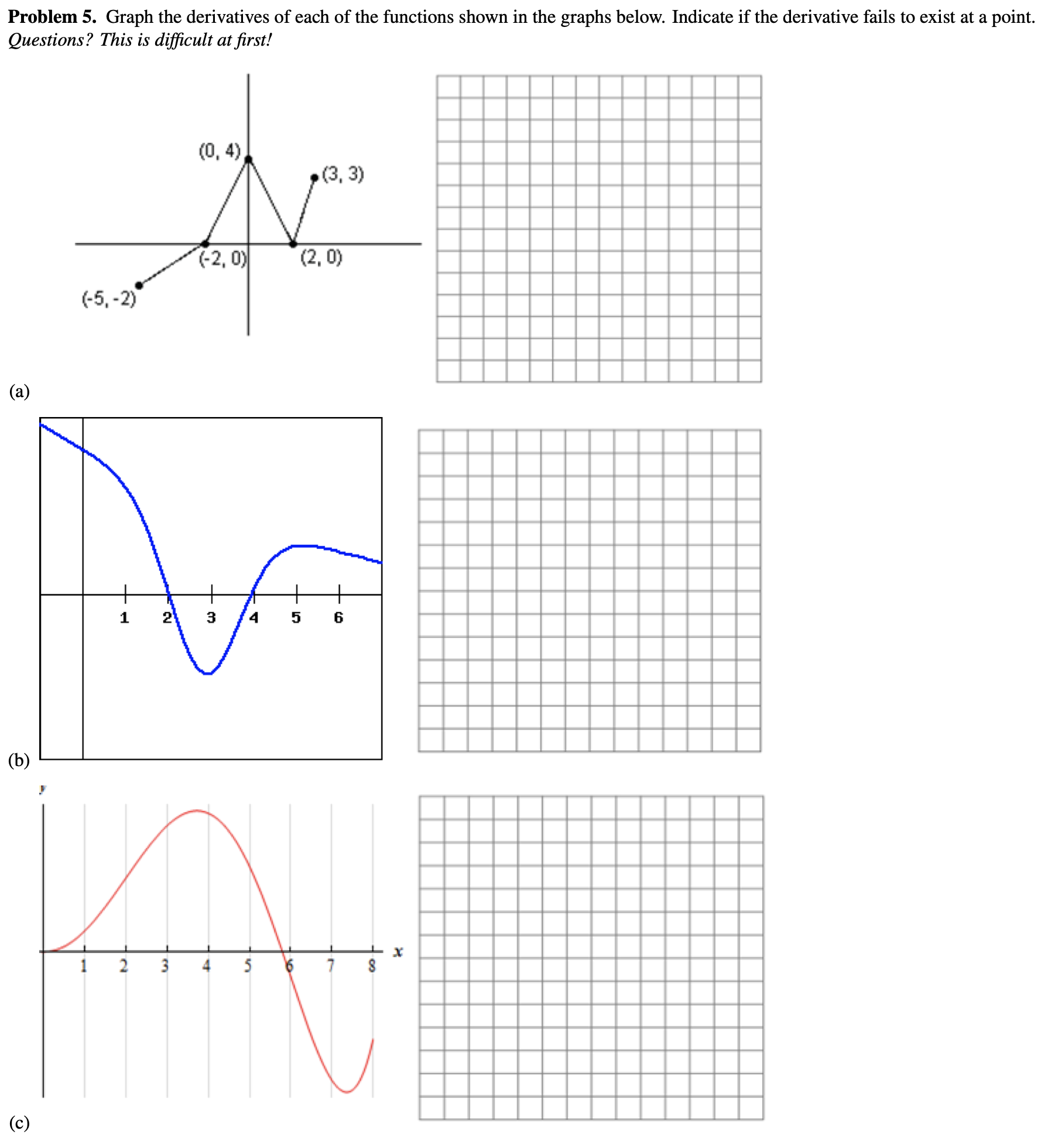
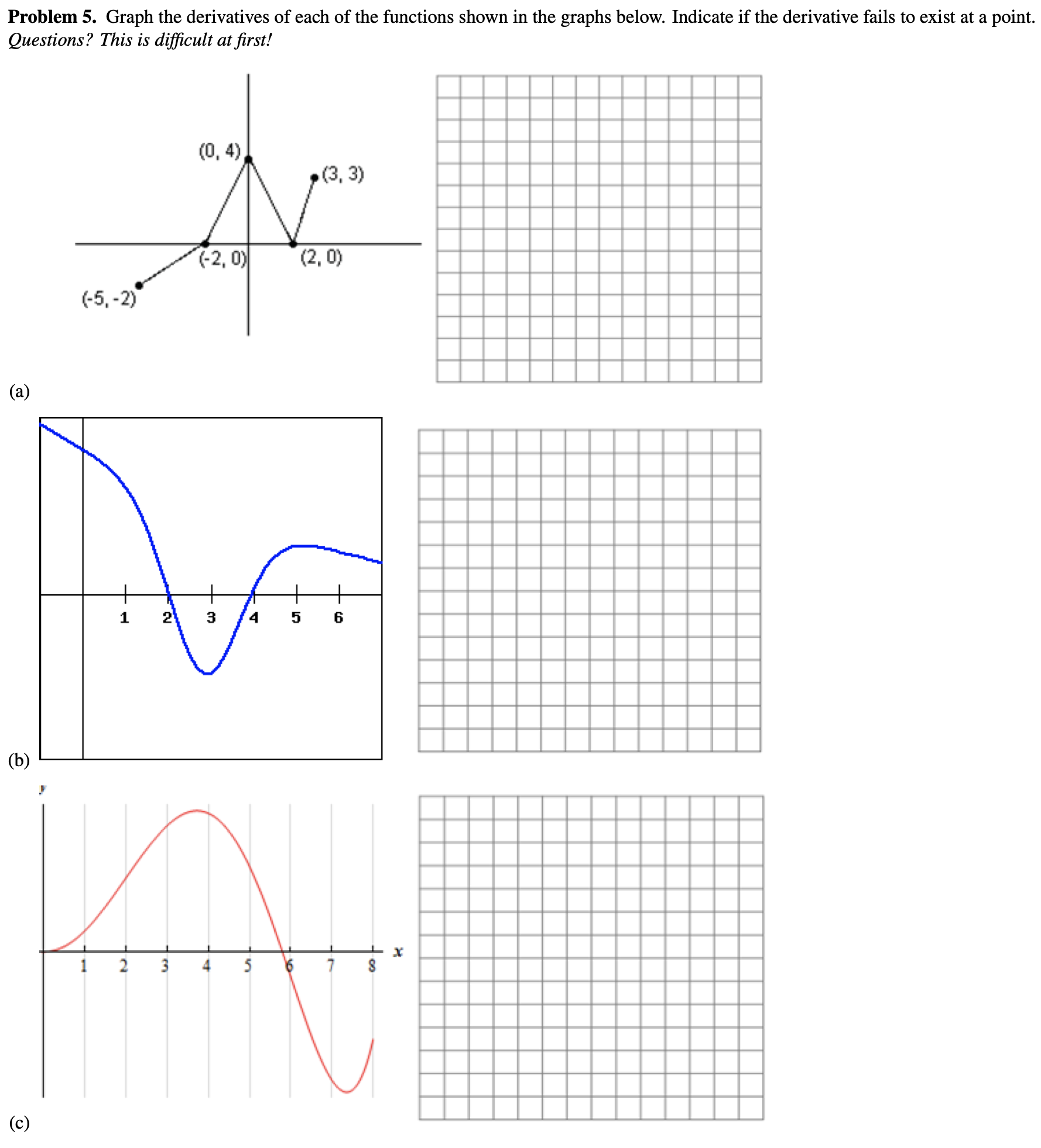
Problem 4. Let f(x) = 3 * Vx. (a) Find f'(x) using derivative rules. (b) Verify your calculation by finding f'(x) using the limit definition of derivative.(c) Calculate f' (4). (d) Find the equation of the line perpendicular (or "normal" in physics) to the curve y = 3 * V)? at the point (4, f (4)). Problem 5. Graph the derivatives of each of the functions shown in the graphs below. Indicate if the derivative fails to exist at a point. Questions? This is difficult at first! (0, 4) (3, 3) (-2, 0) (2, 0) (-5,-2) (a) (b) (c )Problem 6. Find the x-value(s) where g(x) = x - 3x2 - 45x + 19 has horizontal tangent line(s). You can use this Desmos graph if you get stuck or to check your answer: https://www.desmos.com/calculator/ytxhis13rb Drag the slider for a to change the point at which the black line is tangent to the graph of g(x). Problem 7. Find an 8 (x ) dx (x) if h(x) = 2x+ f (x) Your answer should have " and 42 in it. Problem 8. If f (x) = (x + 8)(x - 5) (x2+4) find f' (x).Problem 9. Using the digits 1 to 9 at most one time each, 1. Fill in the boxes to create a function f (x) so that line tangent to it at x = 1 has positive slope f(x)=x 2. Fill in the boxes to create a function so that f ' (1)