Question: Problem 4: Suppose that $P(Y=1 )=P(Y=-1)=1 / 2$. Define $$ Y_{n}=left{begin{array}{11} Y & text { with probability } 1-frac{1}{n} e^{n} & text { with probability

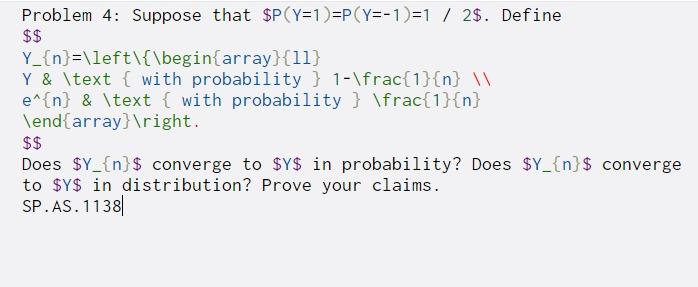
$Problem 4: Suppose that $P(Y=1 )=P(Y=-1)=1 / 2$. Define $$ Y_{n}=\left\{\begin{array}{11}$

Problem 4: Suppose that $P(Y=1 )=P(Y=-1)=1 / 2$. Define $$ Y_{n}=\left\{\begin{array}{11} Y & \text { with probability } 1-\frac{1}{n} e^{n} & \text { with probability } \frac{1}{n} \end{array} ight. $$ Does $Y_{n}$ converge to $y$ in probability? Does $Y_{n}$ converge to $y$ in distribution? Prove your claims. SP.AS. 1138

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

1. A player throws a fair die and simultaneously flips a fair coin. If the coin lands heads, then she wins twice, and if tails, then one-half of the value that appears on the die. Determine her...

Portray in words what transforms you would have to make to your execution to some degree (a) to accomplish this and remark on the benefits and detriments of this thought.You are approached to compose...

Prolog You are approached to compose a Prolog program to work with twofold trees. Your code shouldn't depend on any library predicates and you ought to expect that the mediator is running without...

CANMNMM January of this year. (a) Each item will be held in a record. Describe all the data structures that must refer to these records to implement the required functionality. Describe all the...

I need the answer of question number 5 and 6. I need specific process of the solutions. Homework 3 UNIVERSITY OF MINNESOTA ECON 4751 - Financial Economics Due Thursday, February 25, 2016...

stat5102 HW5 Each problem worths 20 points. Problem 1. Let Y1 Bin(2007, p). (a) Compute the Fisher information I1 (p). (b) Let W (Y1 ) represent an unbiased estimator of p. Use the Information...

Problem 3 Suppose M is a DFA, p and q are states, and a is an input symbol. Argue that if p =m q, then (p, a) =(q, a). (Advice: the contrapositive may be easier.) Problem 4 Suppose M is a DFA, L =...

Exercise Set 6.3: Rules of Probability 1. If a fair die is tossed once, find the probability that the uppermost face displays a(n): 5. and P ( E F ) = 0.19 . Find the following: A. 2 or a 6 A. P ( E...

Kindly solve the following questions. Production Problem 1. Consider the Cobb-Douglas production function f(x,y) = 12x0.4y0.8. (A) Find the intensities (? and 1 ? ?) of the two factors of production....

Business Statistics ( MTH 105) Assignment #1 Student Name: Student ID: Section: 1 Problem 1: A construction company has submitted bids on two separate state contracts, A and B. The company feels that...

Consider the following reactions (unbalanced); Zn + hot conc. H2SO4 ? G + R + X Zn + conc. NaOH ? T + Q G + H2S + NH4OH ? Z (a precipitate) + X + Y Choose the correct option(s) (a) Z is dirty white...

Is there enough evidence to infer that age and the amount of time needed to complete the questionnaire are linearly related in Exercise 16.8?

If the Accounts Recelvabie balance is $ 1 0 milion less than the balance at the beginning of the year, then on the statement of cash flows ( indirect method ) $ 1 0 million should be added to...

help me with this one please, thanks All contracts that are to be settled in the entity's own equity instruments are considered as equity instruments. Select one True O False

2. What are the advantages and disadvantages of job sharing from the companys perspective?

2. Discuss how these future trends may impact training delivery and administration as well as the strategic role of the training department.

1. Identify the future trends that are likely to influence training departments and trainers.