Problem 4-07 (Algorithmic)

As part of the settlement for a class action lawsuit, Hoxworth Corporation must provide sufficient cash to make the following annual payments (in thousands of dollars):

Year	1	2	3	4	5	6
Payment	175	230	300	320	350	480

The annual payments must be made at the beginning of each year. The judge will approve an amount that, along with earnings on its investment, will cover the annual payments. Investment of the funds will be limited to savings (at 4.05% annually) and government securities, at prices and rates currently quoted in The Wall Street Journal.

Hoxworth wants to develop a plan for making the annual payments by investing in the following securities (par value = $1000). Funds not invested in these securities will be placed in savings.

Security	Current Price	Rate (%)	Years to Maturity
1	$1025	6.25	3
2	$1000	5.125	4

Assume that interest is paid annually. The plan will be submitted to the judge and, if approved, Hoxworth will be required to pay a trustee the amount that will be required to fund the plan.

Use linear programming to find the minimum cash settlement necessary to fund the annual payments.

Let
	F = total funds required to meet the six years of payments
	G1 = units of government security 1
	G2 = units of government security 2
	Si = investment in savings at the beginning of year i

Note: All decision variables are expressed in thousands of dollars. If required, round your answers to four decimal places. For subtractive or negative numbers use a minus sign even if there is a + sign before the blank. (Example: -300)

Problem 4-07 (Algorithmic)

As part of the settlement for a class action lawsuit, Hoxworth Corporation must provide sufficient cash to make the following annual payments (in thousands of dollars):

Year	1	2	3	4	5	6
Payment	175	230	300	320	350	480

The annual payments must be made at the beginning of each year. The judge will approve an amount that, along with earnings on its investment, will cover the annual payments. Investment of the funds will be limited to savings (at 4.05% annually) and government securities, at prices and rates currently quoted in The Wall Street Journal.

Hoxworth wants to develop a plan for making the annual payments by investing in the following securities (par value = $1000). Funds not invested in these securities will be placed in savings.

Security	Current Price	Rate (%)	Years to Maturity
1	$1025	6.25	3
2	$1000	5.125	4

Assume that interest is paid annually. The plan will be submitted to the judge and, if approved, Hoxworth will be required to pay a trustee the amount that will be required to fund the plan.

1. Use linear programming to find the minimum cash settlement necessary to fund the annual payments.

   Let
   	F = total funds required to meet the six years of payments
   	G1 = units of government security 1
   	G2 = units of government security 2
   	Si = investment in savings at the beginning of year i

   Note: All decision variables are expressed in thousands of dollars. If required, round your answers to four decimal places. For subtractive or negative numbers use a minus sign even if there is a + sign before the blank. (Example: -300)

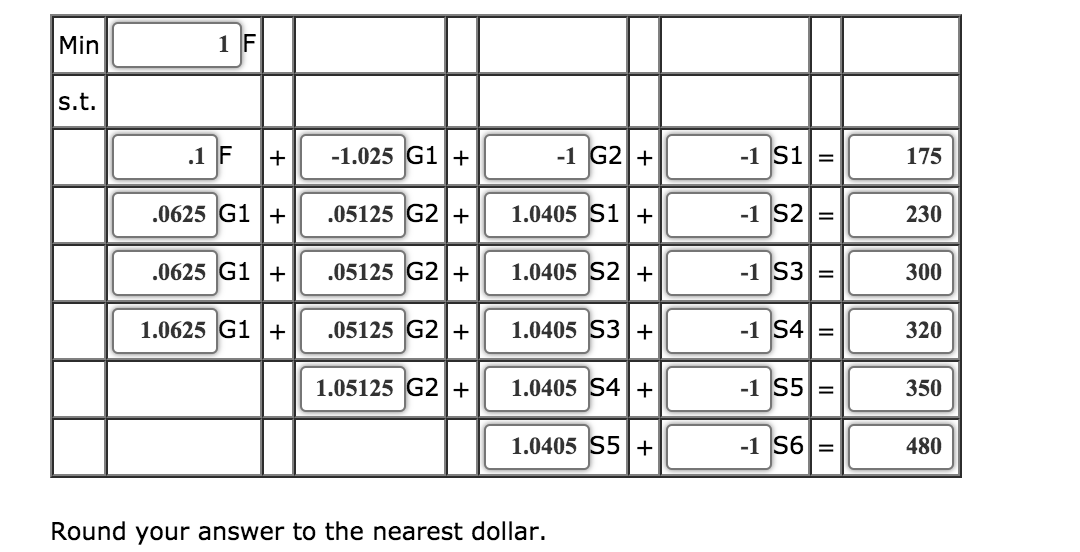
   Min	fill in the blank 1F
   s.t.
   	fill in the blank 2F	+	fill in the blank 3G1	+	fill in the blank 4G2	+	fill in the blank 5S1	=	fill in the blank 6
   	fill in the blank 7G1	+	fill in the blank 8G2	+	fill in the blank 9S1	+	fill in the blank 10S2	=	fill in the blank 11
   	fill in the blank 12G1	+	fill in the blank 13G2	+	fill in the blank 14S2	+	fill in the blank 15S3	=	fill in the blank 16
   	fill in the blank 17G1	+	fill in the blank 18G2	+	fill in the blank 19S3	+	fill in the blank 20S4	=	fill in the blank 21
   			fill in the blank 22G2	+	fill in the blank 23S4	+	fill in the blank 24S5	=	fill in the blank 25
   					fill in the blank 26S5	+	fill in the blank 27S6	=	fill in the blank 28

   Round your answer to the nearest dollar.

   Current investment required	$ fill in the blank 29
   Investment in government security 1	$ fill in the blank 30
   Investment in government security 2	$ fill in the blank 31
   Investment in savings for year 1	$ fill in the blank 32
   Investment in savings for year 2	$ fill in the blank 33
   Investment in savings for year 3	$ fill in the blank 34
   Investment in savings for year 4	$ fill in the blank 35
   Investment in savings for year 5	$ fill in the blank 36
   Investment in savings for year 6	$ fill in the blank 37

2. Use the shadow price to determine how much more Hoxworth should be willing to pay now to reduce the payment at the beginning of year 6 to $400,000. Round your answer to the nearest dollar. $______
3. Use the shadow price to determine how much more Hoxworth should be willing to pay to reduce the year 1 payment to $150,000. Round your answer to the nearest dollar. Hoxworth should be willing to pay anything less than $_______
4. Suppose that the annual payments are to be made at the end of each year. Reformulate the model to accommodate this change. Note: All decision variables are expressed in thousands of dollars. If required, round your answers to four decimal places. For subtractive or negative numbers use a minus sign even if there is a + sign before the blank. (Example: -300)

Min 1 F s.t. .1 F + -1.025 G1+ -1 G2+ -1 S1 = 175 .0625 G1 + .05125 G2+ 1.0405 S1+ -1 S2 = 230 .0625 G1 + .05125 G2+ 1.0405 S2+ -1 S3= 300 1.0625 G1 + .05125 G2+ 1.0405 S3+ -1 S4= 320 1.05125 G2+ 1.0405 S4+ -1 S5= 350 1.0405 55+ -1 S6= 480 Round your answer to the nearest dollar. Round your answer to the nearest dollar. Current investment required $ 1609821 Investment in government security 1 263950 Investment in government security 2$ 771764 Investment in savings for year 1 392508 Investment in savings for year 2 $ $ $ 234455 Investment in savings for year 3 0 Investment in savings for year 4 0 Investment in savings for year 5 $ 461317 Investment in savings for year 6 $ 0 b. Use the shadow price to determine how much more Hoxworth should be willing to pay now to reduce the payment at the beginning of year 6 to $400,000. Round your answer to the nearest dollar. 80000 If required, round your answers to four decimal places. For subtractive or negative numbers use a minus sign even if there is a + sign before the blank. (Example: -300) Min F s.t. 1) F + G1+ G2+ S1 = 2) G1+ G2+ S1+ S2= 3) G1+ G2+ S2+ S3= 4) G1+ G2+ S3+ S4= 5) G2+ S4+ S5= 6) S5+ S6= 7) S6+ S7= How much would Hoxworth save if this change could be negotiated? Round your answer to the nearest dollar. Min 1 F s.t. .1 F + -1.025 G1+ -1 G2+ -1 S1 = 175 .0625 G1 + .05125 G2+ 1.0405 S1+ -1 S2 = 230 .0625 G1 + .05125 G2+ 1.0405 S2+ -1 S3= 300 1.0625 G1 + .05125 G2+ 1.0405 S3+ -1 S4= 320 1.05125 G2+ 1.0405 S4+ -1 S5= 350 1.0405 55+ -1 S6= 480 Round your answer to the nearest dollar. Round your answer to the nearest dollar. Current investment required $ 1609821 Investment in government security 1 263950 Investment in government security 2$ 771764 Investment in savings for year 1 392508 Investment in savings for year 2 $ $ $ 234455 Investment in savings for year 3 0 Investment in savings for year 4 0 Investment in savings for year 5 $ 461317 Investment in savings for year 6 $ 0 b. Use the shadow price to determine how much more Hoxworth should be willing to pay now to reduce the payment at the beginning of year 6 to $400,000. Round your answer to the nearest dollar. 80000 If required, round your answers to four decimal places. For subtractive or negative numbers use a minus sign even if there is a + sign before the blank. (Example: -300) Min F s.t. 1) F + G1+ G2+ S1 = 2) G1+ G2+ S1+ S2= 3) G1+ G2+ S2+ S3= 4) G1+ G2+ S3+ S4= 5) G2+ S4+ S5= 6) S5+ S6= 7) S6+ S7= How much would Hoxworth save if this change could be negotiated? Round your answer to the nearest dollar