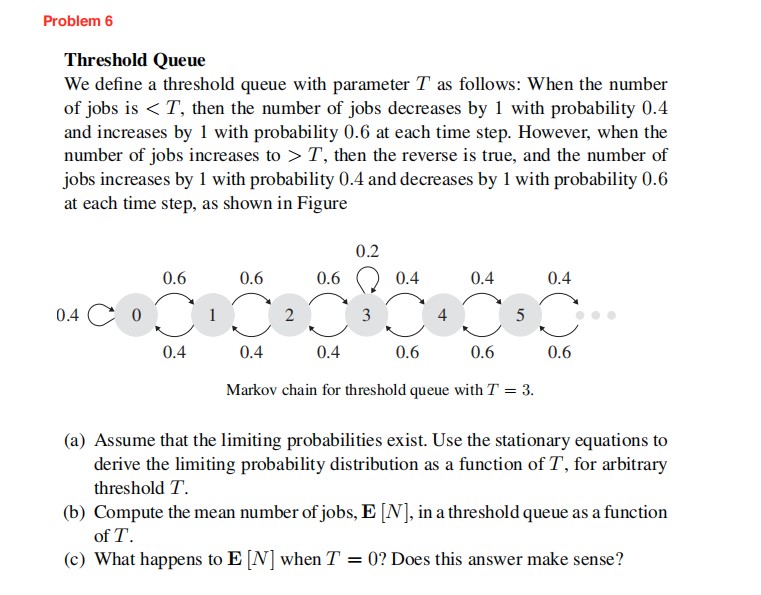
Problem 5 Threshold Queue We dene a mreshold queue with parameter T as follows: When the number of jobs is ti T, then the number of jobs decreases by l wilh probability [L4 and increases by l with probability [L6 at each time step. However, when the number of jobs increases to 2} T, then the reverse is true, and the number of jobs increases by l with probability [)4 and decreases by l with probability [Hi at each time step, as shown in Figure ca no no () 04 n4 o4 04(:3 o 1 2 3 4 5 ad; aux aux aux aux aux n4 n4 n4 no no no Markov chain for threshold queue with T = 3. (a) Assume that the limiting probabilities exist, Use the stationary equations to derive the limiting probability distribution as a function of T, for arbitrary mreshold T, (b) Compute the mean number ofjobs, E [N], in a threshold queue as a function of T, (c) What happens to E [N] when T = 0'? Does this answer make sense