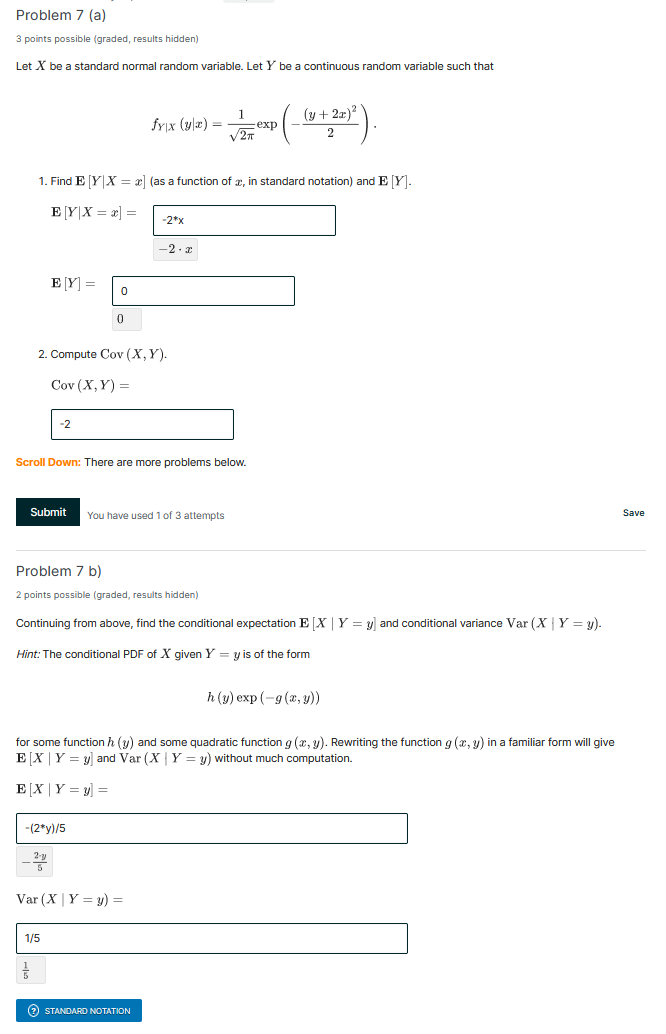
Problem 7 (a) 3 points possible (graded, results hidden) Let X be a standard normal random variable. Let Y be a continuous random variable such that frix (y x) = 1 (y + 2x)2 exp V2AT 2 1. Find E [Y| X = ] (as a function of x, in standard notation) and E [Y]. E YX= = .2*x -2 . E EYE 0 2. Compute Cov (X, Y). Cov (X, Y) = -2 Scroll Down: There are more problems below. Submit You have used 1 of 3 attempts Save Problem 7 b) 2 points possible (graded, results hidden) Continuing from above, find the conditional expectation E [X | ) = y] and conditional variance Var (X | Y = y). Hint: The conditional PDF of X given Y" = y is of the form h (y) exp (-g (x, y)) for some function h (y) and some quadratic function g (@, y). Rewriting the function g (x, y) in a familiar form will give EX | Y = y] and Var (X | Y = y) without much computation. EX Y = y] = -(2*y)/5 Var (X | Y = y) = 1/5 (?) STANDARD NOTATION