Problem 7-02 (Algorithmic)

Consider the following all-integer linear program:
		Max	5x1	+	8x2
		s.t.
			5x1	+	6x2		32
			10x1	+	5x2		46
			x1	+	2x2		10
x1, x2 0						and integer

Choose the correct graph which shows the constraints for this problem and uses dots to indicate all feasible integer solutions.

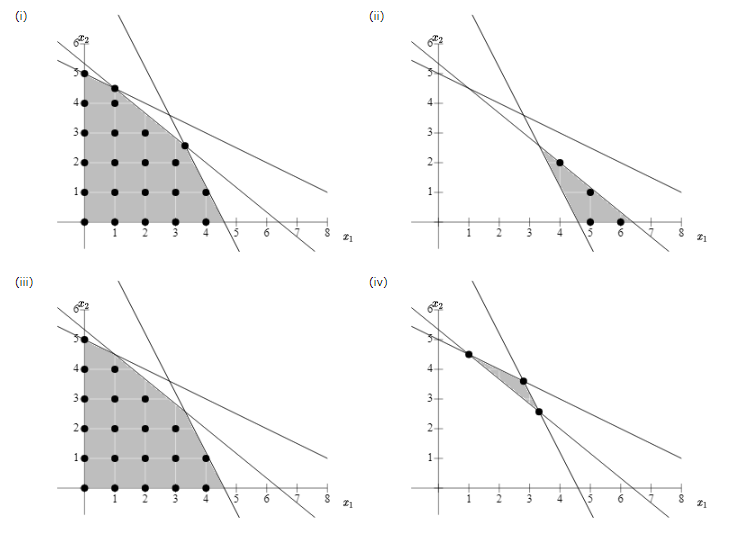
Graph (i)Graph (ii)Graph (iii)Graph (iv)

Find the optimal solution to the LP Relaxation. If required, round your answers to two decimal places.

x1=	fill in the blank 2
x2=	fill in the blank 3
Optimal Solution to the LP Relaxation	fill in the blank 4

Round down to find a feasible integer solution. If your answer is zero enter 0.

x1=	fill in the blank 5
x2=	fill in the blank 6
Feasible integer solution	fill in the blank 7

Find the optimal integer solution. If your answer is zero enter 0.

x1=	fill in the blank 8
x2=	fill in the blank 9
Optimal Integer Solution	fill in the blank 10

Is it the same as the solution obtained in part (b) by rounding down?

(i) (ii) (iii) (iv)