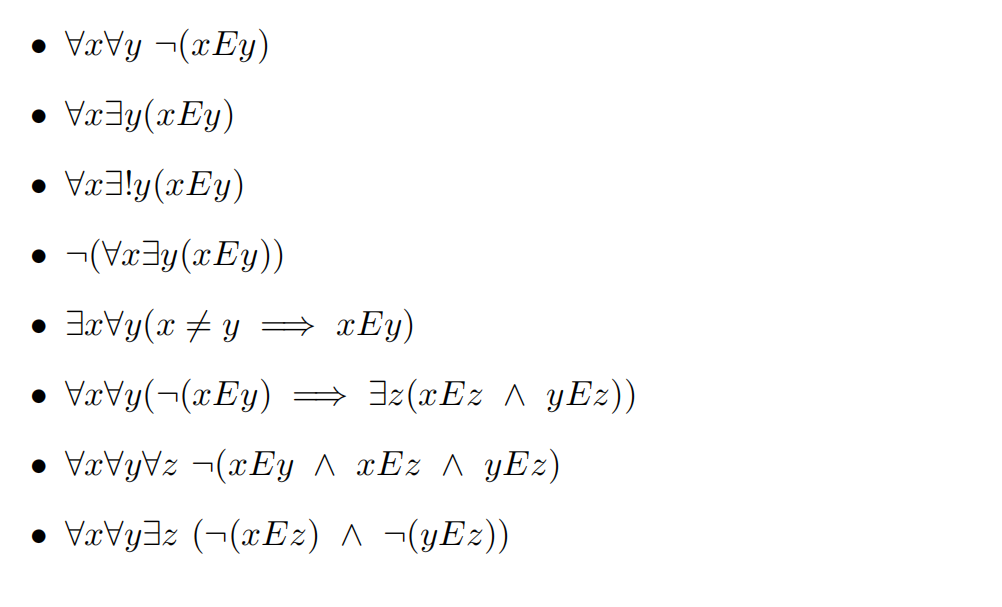
Problem 8. A graph! consists of a set V along with a irreflexive,? symmetric relation on V. We represent graphs by drawing each of the elements of V' as vertices or nodes and if v1,v2 V such that v1 Fvy we draw an edge between the vertex v; and vs. For example, let G; be the graph consisting of V' = {a,b,c,d} and F, = {(a,b), (b,a),(a,c),(c,a),(b,c),(c,b),(b,d),(d,b)}. Let G5 be the graph consist- ing of V = {a,b,c,d} and Ey = {(a,b), (b,a),(a,c),(c,a),(c,d),(d,c)}. Let G be the graph consisting of V3 = {1,2,3,4,5} and E3 = V3 xV3\\{(z,z) : z V3}. We can represent the graphs G, G5, and G3 by the following diagrams: 5/1\\2 & b ig |/ \\Q/ baeg 8 For each of the following sentences, explain in your own words what the sentence says and give an example of a graph in which the sentence is true. No proof is required. Feel free to draw pictures. o VaVy(x #y = zEy) \f