Problem C Only

A = 6, B = 6, C = 8, D = 9, E = 7

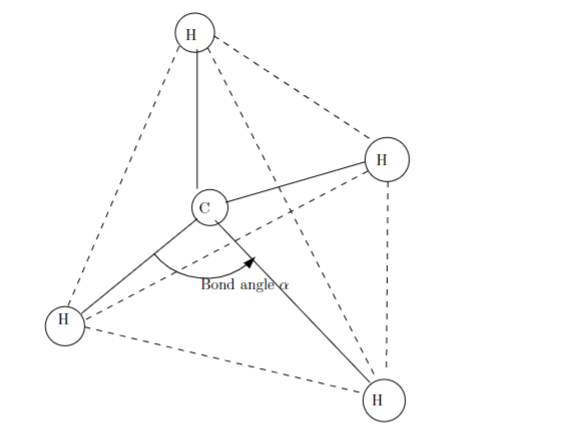
For Problem 2 Part C, the points of the tetrahedron are for (0,0,0),(c,c,0),(c,0,c), and (0,c,c). THE METHANE MOLECULE CH4. Part a) Prove that the points (0,0,0),(a,a,0),(a,0,a), and (0,a,a) are the vertices of a regular tethrahedron by showing that each of the six edges has length 2a. Then use the dot product to find the angle between any two edges of the tetrahedron. Part b) The methane molecule CH4 is arranged with the four hydrogen (H) atoms at the vertices of the tetrahedron of Part a) above with the carbon (C) atom at its center. Suppose that the center is at (2a,2a,2a). Find the bond angle between the lines from the carbon atom to two of the hydrogen atoms. (See Figure 1 below) Part c) Suppose you discovered this (unlikely) methane-like molecule CABEF where the center is still occupied by a carbon atom C and the vertices are occupied by atoms A,B,E, and F that are at the same positions as the previous hydrogen atoms. If the carbon atom is to be located at (x,2cx,2c), minimize the bond angle between the carbon atom and the A and B atoms