Problem Description: Consider the vertical motion of a rocket. Initially, its altitude, velocity, and mass are 0.0 m, 0.0 m/s, and m0 kg, respectively. After it is launched, the rocket's altitude ( h ), velocity ( v ), and mass ( m ) are governed by the following system of three ordinary differential equations (ODEs): Note: 1. the rate of fuel consumption phi is a non-zero constant ( phi0 ) before the fuel is completely burned, and zero afterward. 2. The rocket carries a parachute which is programmed to deploy at time t1. The value of drag coefficient c_d is cd_0 before time t1, and increases to cd_1 afterwards. Using the Euler's Method, the above differential equations are converted into a system of step-by-step, algebraic equations:

This is what I have, but it is not correct. Thank you!

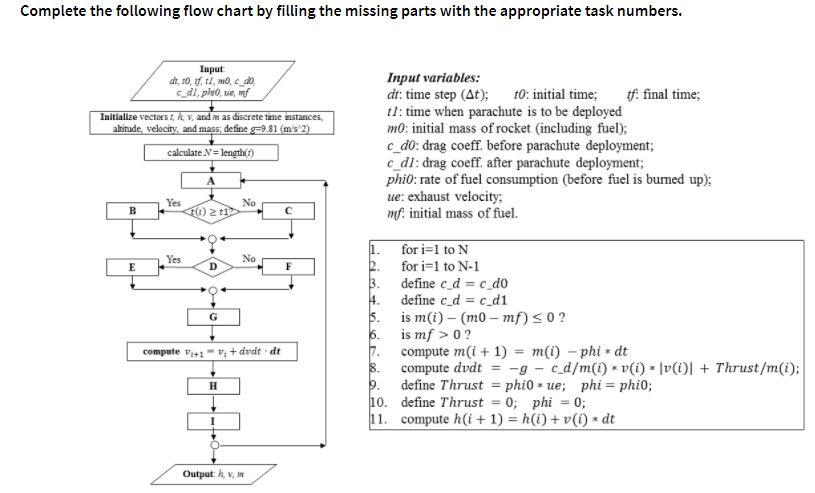
A = 2; B = 4; C = 3; D = 6; E = 9; F = 10; G = 8; H = 11; I = 7;

Complete the following flow chart by filling the missing parts with the appropriate task numbers Input variables dt: time step (At); t0: initial time;final time: t: time when parachute is to be deployed m0: initial mass of rocket (including fuel); c d0: drag coeff. before parachute deployment; c dl: drag coeff. after parachute deployment phi0: rate of fuel consumption (before fuel is burned up); ue: exhaust velocity; mf. initial mass of fuel. Initialize vectors, h, s. and e tme nstances as define g-9.81 (m's 2 calculate N length) Yes for i-1 to N for i-1 to N-1 define c-d-c-d0 define c-d-c-d1 is m(i) - (m0- mf) s0 is mf> 0? compute m(i + 1) = m()-phi * dt compute dvdt -g-c-d/m(i) * v(i) * |v(i)| + Thrust/m(1); define Thrust = phi0 * ue ; phi = phi0; Yes No compute vi1- dvdt dt 0, define Thrust= 0; phi=0; 1. compute h(i 1)- h(i) + v(i) dt Output: h, v