problem f only, using julia programming language

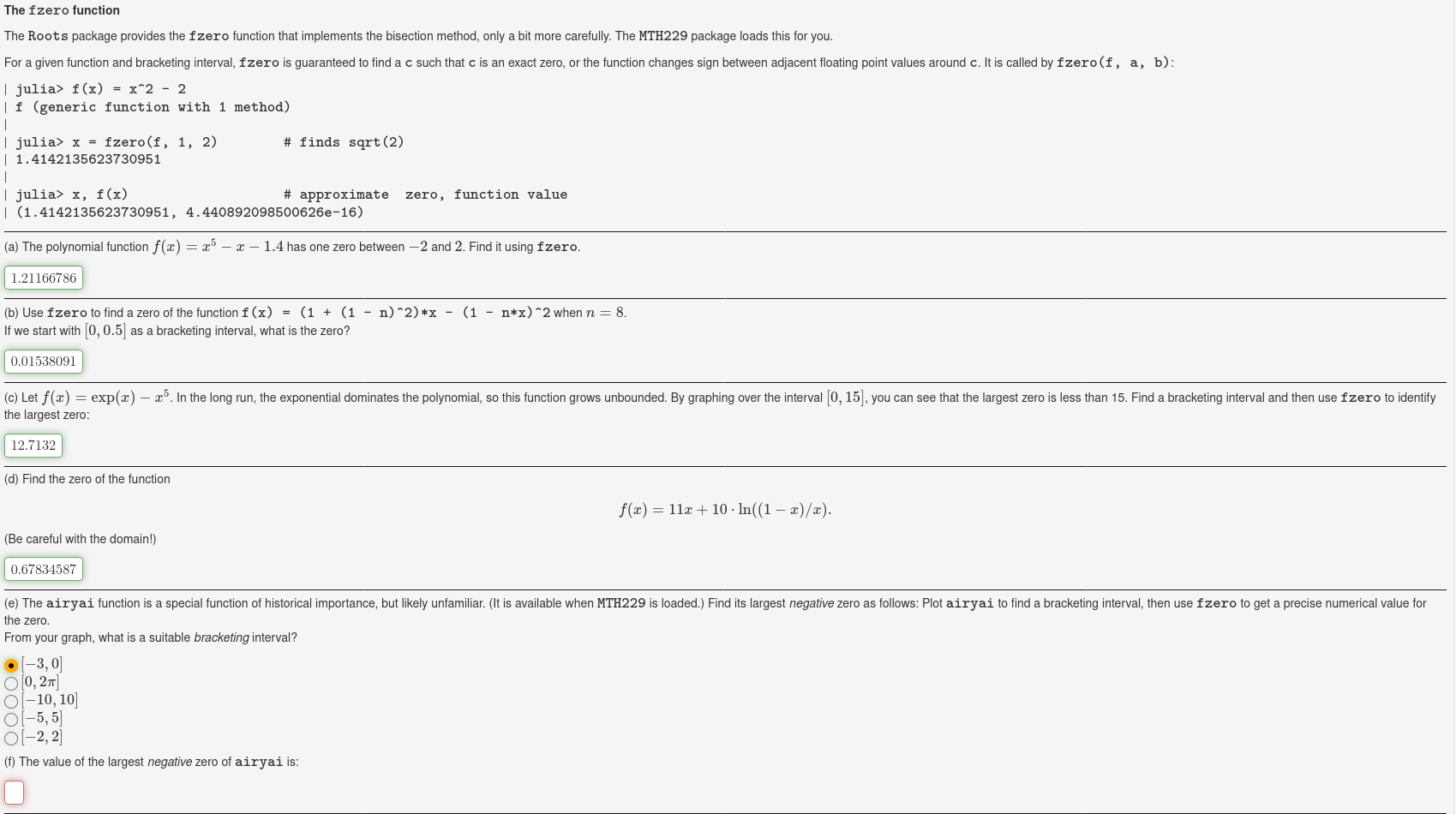
The fzero function The Roots package provides the fzero function that implements the bisection method, only a bit more carefully. The MTH229 package loads this for you. For a given function and bracketing interval, fzero is guaranteed to find a c such that c is an exact zero, or the function changes sign between adjacent floating point values around c. It is called by fzero(f, a, b): | julia> f(x) = x^2 - 2 | f (generic function with 1 method) 1 | julia> x = fzero(f, 1, 2) # finds sqrt(2) | 1.4142135623730951 1 | julia> x, f(x) # approximate zero, function value | (1.4142135623730951, 4.440892098500626e-16) (a) The polynomial function f(x) = x - x - 1.4 has one zero between-2 and 2. Find it using fzero. 1.21166786 (b) Use fzero to find a zero of the function f(x) = (1 + (1 - n)-2)*x - (1 - n*x) 2 when n = 8. If we start with (0, 0.5] as a bracketing interval, what is the zero? 0.01538091 (C) Let f(0) = exp(2) 25. In the long run, the exponential dominates the polynomial, so this function grows unbounded. By graphing over the interval (0, 15), you can see that the largest zero is less than 15. Find a bracketing interval and then use fzero to identify the largest zero: 12.7132 (d) Find the zero of the function f(x) = 11x + 10. In((1 )/x). (Be careful with the domain!) 0.67834587 (e) The airyai function is a special function of historical importance, but likely unfamiliar. (It is available when MTH229 is loaded.) Find its largest negative zero as follows: Plot airyai to find a bracketing interval, then use fzero to get a precise numerical value for the zero. From your graph, what is a suitable bracketing interval? (-3,0 O 0,25 Ol-10,10) O(-5,5) Of-2,2 (f) The value of the largest negative zero of airyai is: The fzero function The Roots package provides the fzero function that implements the bisection method, only a bit more carefully. The MTH229 package loads this for you. For a given function and bracketing interval, fzero is guaranteed to find a c such that c is an exact zero, or the function changes sign between adjacent floating point values around c. It is called by fzero(f, a, b): | julia> f(x) = x^2 - 2 | f (generic function with 1 method) 1 | julia> x = fzero(f, 1, 2) # finds sqrt(2) | 1.4142135623730951 1 | julia> x, f(x) # approximate zero, function value | (1.4142135623730951, 4.440892098500626e-16) (a) The polynomial function f(x) = x - x - 1.4 has one zero between-2 and 2. Find it using fzero. 1.21166786 (b) Use fzero to find a zero of the function f(x) = (1 + (1 - n)-2)*x - (1 - n*x) 2 when n = 8. If we start with (0, 0.5] as a bracketing interval, what is the zero? 0.01538091 (C) Let f(0) = exp(2) 25. In the long run, the exponential dominates the polynomial, so this function grows unbounded. By graphing over the interval (0, 15), you can see that the largest zero is less than 15. Find a bracketing interval and then use fzero to identify the largest zero: 12.7132 (d) Find the zero of the function f(x) = 11x + 10. In((1 )/x). (Be careful with the domain!) 0.67834587 (e) The airyai function is a special function of historical importance, but likely unfamiliar. (It is available when MTH229 is loaded.) Find its largest negative zero as follows: Plot airyai to find a bracketing interval, then use fzero to get a precise numerical value for the zero. From your graph, what is a suitable bracketing interval? (-3,0 O 0,25 Ol-10,10) O(-5,5) Of-2,2 (f) The value of the largest negative zero of airyai is