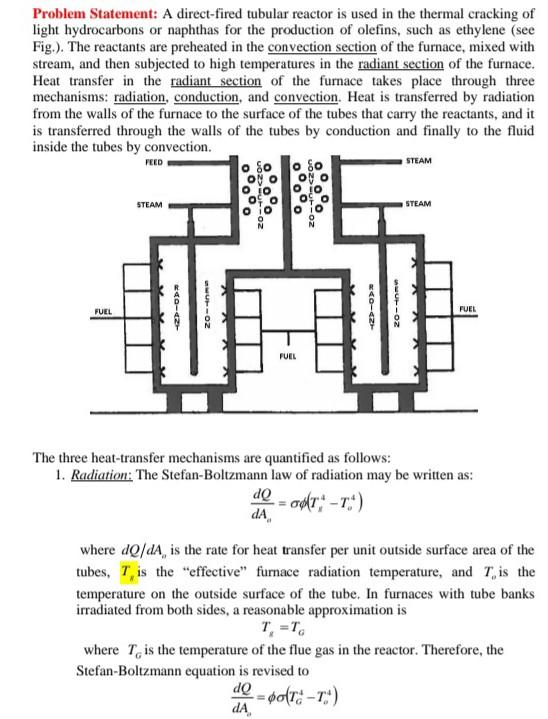
Problem Statement: A direct-fired tubular reactor is used in the thermal cracking of light hydrocarbons or naphthas for the production of olefins, such as ethylene (see Fig.). The reactants are preheated in the convection section of the furnace, mixed with stream, and then subjected to high temperatures in the radiant section of the furnace. Heat transfer in the radiant section of the furnace takes place through three mechanisms: radiation, conduction, and convection. Heat is transferred by radiation from the walls of the furnace to the surface of the tubes that carry the reactants, and it is transferred through the walls of the tubes by conduction and finally to the fluid inside the tubes by convection. PEED STEAM STEAM STEAM FUEL O-2 WOZ 0-2 FUEL 20- FUEL The three heat-transfer mechanisms are quantified as follows: 1. Radiation: The Stefan-Boltzmann law of radiation may be written as: dQ odr-14) dA where dg/dA, is the rate for heat transfer per unit outside surface area of the tubes, T, is the "effective" furnace radiation temperature, and T, is the temperature on the outside surface of the tube. In furnaces with tube banks irradiated from both sides, a reasonable approximation is T, ET where T. is the temperature of the flue gas in the reactor. Therefore, the Stefan-Boltzmann equation is revised to = dA dQ - por: -T) . o is the Stefan-Boltzmann constant and is the tube geometry emissivity factor, which depends on the tube arrangement and tube surface emissivity. For single rows of tubes irradiated from both sides: 11 1 + 202 S - + arctan(z)-Z D where 2 is given by: S Z = -1 D where & is the emissivity of the outside surface of the tube and S is the spacing (pitch) of the tubes (center-to-center) and D, is the outside diameter of the tubes. 2. Conduction: Conduction through the tube wall is given by Fourier equation; dQ _K_(T.-T) DA 1 where T) is the temperature on the inside surface of the tube, k, is the thermal conductivity of the tube material, and t, is the thickness of the tube wall. 3. Convection: Convection through the fluid film inside the tube is expressed by: dQ DA D C)(z-7) 1, 3) " ON where D is the inside diameter of the tube, T, is the temperature of the fluid in the tube, and h, is the film heat transfer coefficient on the inside of the tube. hi may be approximated Nusselt number given by Dittus-Boelter equation as: Nu=0.023 Rey P.; The Nusselt number is given by: Nu =hD. ki Nuxk, Hence, h = = 0.023 Re, Pr D D. where Re , is the fluid Reynolds number, Pr, is the fluid Prandtl number, and k, is the thermal conductivity of the fluid. Conditions vary drastically along the length of the tube, as the temperature of the fluid inside the tubes rises rapidly. The rate of heat transfer is the highest at the entrance conditions and lowest at the exit condition of the fluid. Using the numerical method of your choice and any computational tool, preferably the MATLAB, calculate: 04 (a) Derive the nonlinear algebraic equation (b) The heat flux dg/dA (c) The temperature on the outside surface of the tube T (d) The temperature of the inside surface of the tube, T at a point along the length of the tube where the following conditions exist: To = 1200C T, = 800C E=0.9 o = 5.7x10*W/m..K* S=0.2m D = 0. Im D=0.11m 1, = 0.006m Re, = 388,000 Pr=0.66 k, = 21.6 W/m.K k, = 0,175 W/m.K