Problem Statement

Read and understand The Bigger Picture section on page 337 on The book "Java Programming: From The Ground Up (1st Edition). Be ready to explain why or how the various solutions are different. After you get the code for public class FibTester, which starts on page 341 to work, experiment with different numbers (I recommend keeping nExplain how everything works step by step.

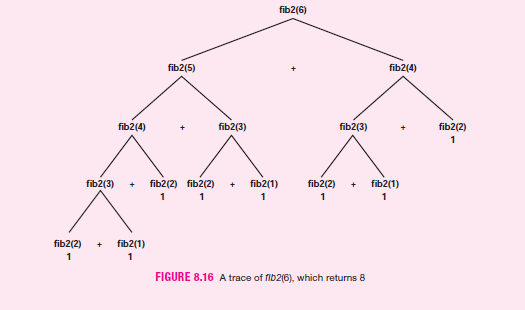
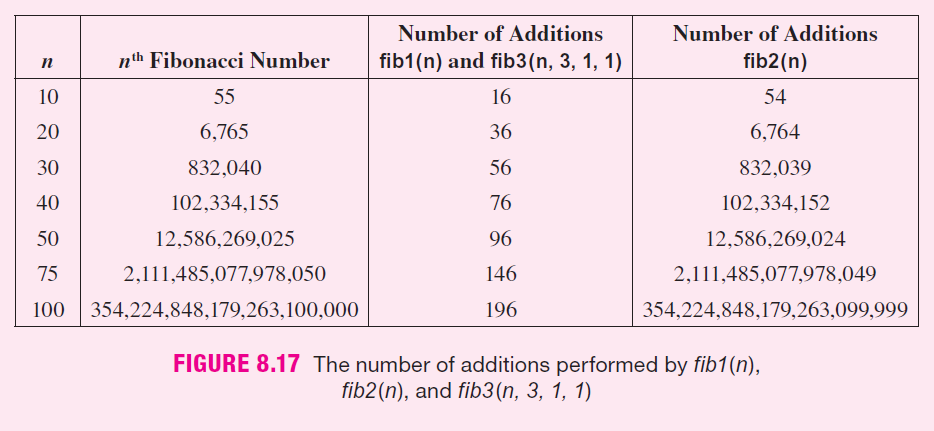
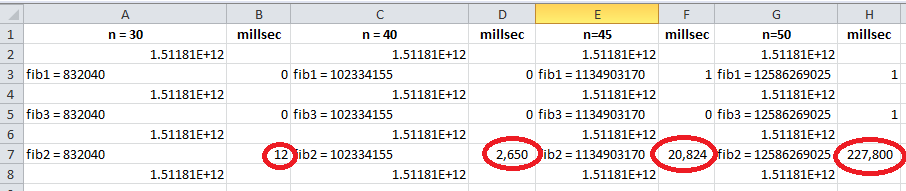
THE BIGGER PICTURE THE COMPLEXITY OF RECURSIVE ALGORITHMS The complexity of an algorithm is synonymous with the speed of an algorithm. Does the algorithm run efficiently, that is, quickly, or not? The faster a program runs, the better; and behind every fast program there is an efficient algorithm. When designing a recur- sive algorithm, it is not only correctness that is important, but efficiency. Let's look at an example. The Fibonacci numbers comprise the infinite sequence: 1, 1. 2, 3. 5, 8, 13, 21. 34, 55, 89, and so on, in which each number (except the first two) is the sum of the previous two numbers. In computer science, Fibonacci numbers have many applications ranging from data structures (Fibonacci heaps) to pseudo-random number generators (lagged Fibonacci generators). Fibonacci numbers also manifest themselves in leaf arrangements, seashells, pine cones, and sunflower seeds. The sunflower in Figure 8.14, for example, has 21 and 34 spirals of seeds, one set curving right and one set curving left. Note that 21 and 34 are the 10th and 11th Fibonacci numbers