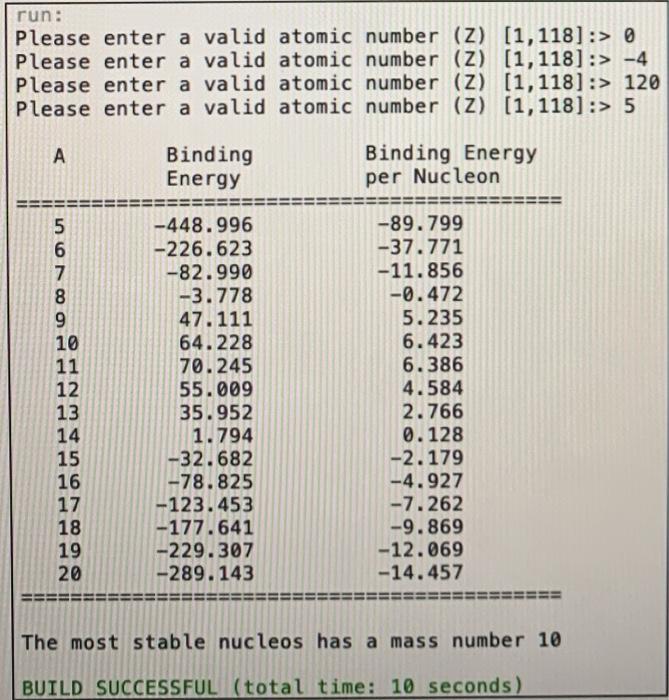
Problem: The nuclear binding energy is the energy required to split a nucleus of an atom in its component parts: protons and neutrons, or, collectively, the nucleons. It describes how strongly nucleons are bound to each other. When a high amount of energy is needed to separate the nucleons, it means nucleus is very stable and the neutrons and protons are tightly bound to each other. + Binding energy required to separate the components Nucleus (Protons + Neutrons) Separated nucleons 2242/2 41/ da + The approximate nuclear binding energy (E.) of an atomic nucleus with atomic number Z and mass number A is calculated using the following formula 2 E = 41A ag - 4-2212 where, a, - 15.67,42 - 1723, a;=0.75, a. = 93.2, and if A is odd as 12.0 if A and Z are both even, -12.0 if A is even and Z is odd. And the binding energy per nucleon (BEN) is calculated by dividing the binding energy (En) by the mass number (4) 0 In this assignment you are asked to write a java program that asks the user for a valid atomic number (Z) then goes through all values of A from A - Z to A - 4Z to find the mass number (4) that has the largest binding energy per nucleon (BEN). If the user enters invalid atomie number that is not between 1 and 118, the program should give the user other chance to enter a valid input. run: Please enter a valid atomic number (Z) (1,118] :> 0 Please enter a valid atomic number (Z) (1,118] :> -4 Please enter a valid atomic number (Z) (1,118] :> 120 Please enter a valid atomic number (Z) (1,118] :> 5 A A Binding Energy Binding Energy per Nucleon u li 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 -448.996 -226.623 -82.990 -3.778 47.111 64.228 70.245 55.009 35.952 1.794 -32.682 -78.825 -123.453 -177.641 -229.307 -289.143 -89.799 -37.771 -11.856 -0.472 5.235 6.423 6.386 4.584 2.766 0.128 -2.179 -4.927 -7.262 -9.869 -12.069 -14.457 The most stable nucleos has a mass number 10 BUILD SUCCESSFUL (total time: 10 seconds)