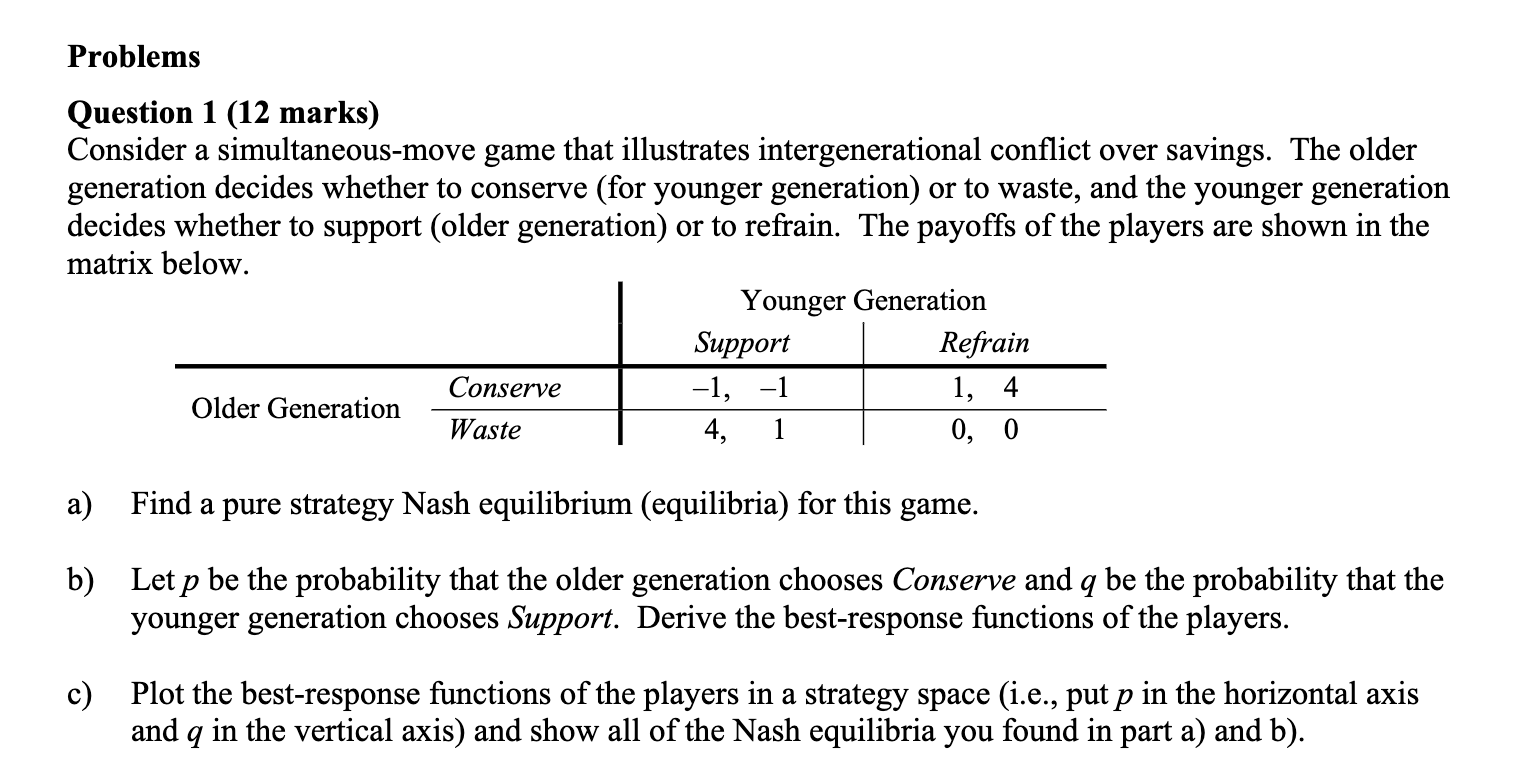
Problems Question 1 (12 marks) Consider a simultaneous-move game that illustrates intergenerational conict over savings. The older generation decides whether to conserve (for younger generation) or to waste, and the younger generation decides whether to support (older generation) or to reain. The payoffs of the players are shown in the matrix below. Younger Generation Older Generation Waste a) Find a pure strategy Nash equilibrium (equilibria) for this game. b) Let p be the probability that the older generation chooses Conserve and g be the probability that the younger generation chooses Support. Derive the best-response functions of the players. c) Plot the best-response functions of the players in a strategy space (i.e., put p in the horizontal axis and q in the vertical axis) and show all of the Nash equilibria you found in part a) and b). Consider a dynamic version of the game. Suppose the older generation moves first. d) Draw a tree diagram of this sequential-move game. What is a subgame perfect Nash equilibrium? e) The method of backward induction eliminates Nash equilibria that involve non-credible threats. Identify the equilibrium. State clearly who made what threat and explain why it is not credible