Produce a code that uses the bisection method to reproduce the image below given the equation below.

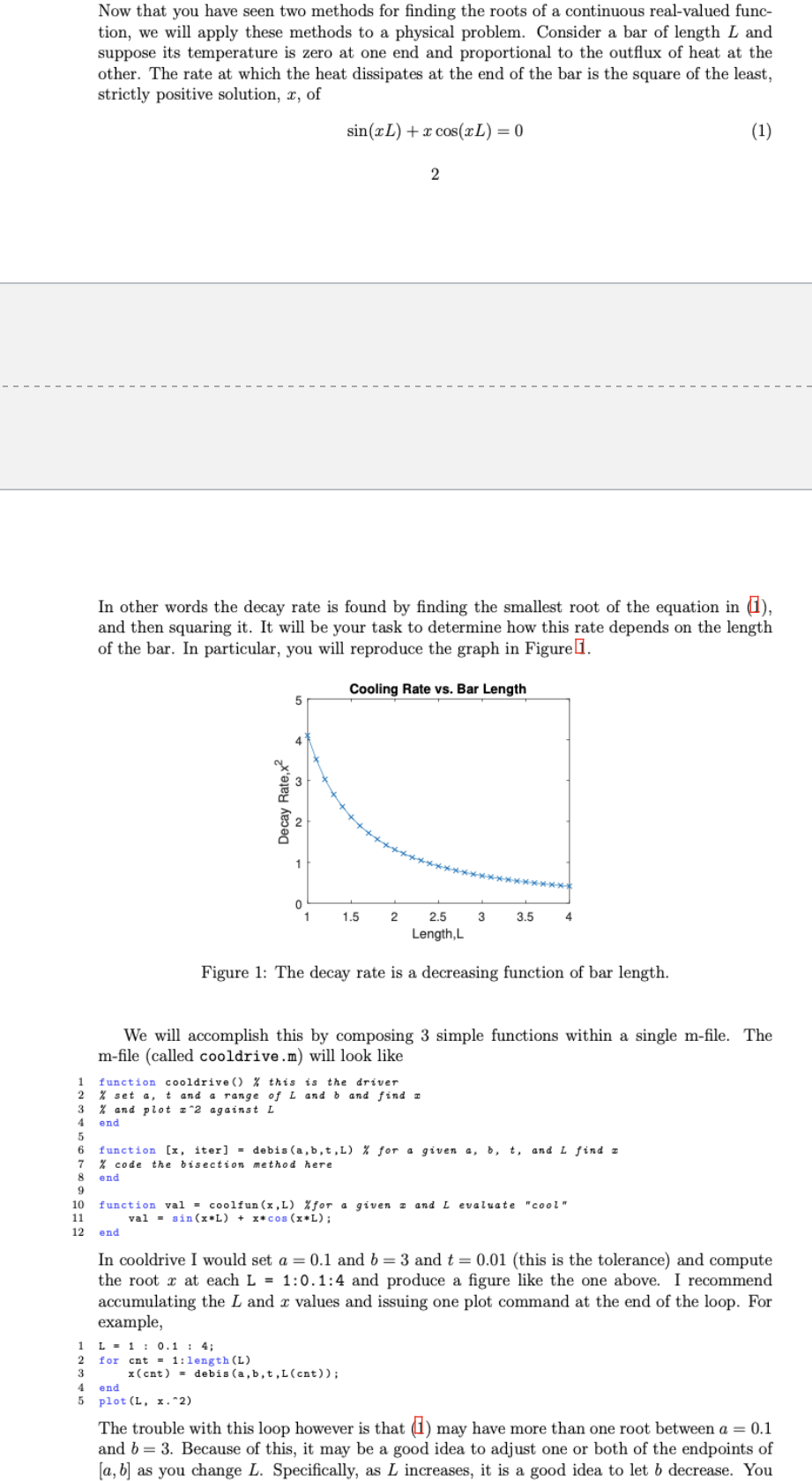
Now that you have seen two methods for finding the roots of a continuous real-valued func- tion, we will apply these methods to a physical problem. Consider a bar of length L and suppose its temperature is zero at one end and proportional to the outflux of heat at the other. The rate at which the heat dissipates at the end of the bar is the square of the least, strictly positive solution, x, of sin(xL) + x cos(xL) = 0) (1) 2 In other words the decay rate is found by finding the smallest root of the equation in ), and then squaring it. It will be your task to determine how this rate depends on the length of the bar. In particular, you will reproduce the graph in Figurei. Cooling Rate vs. Bar Length 5 Decay Rate, 1 0 1 1.5 2 3 3.5 2.5 Length, Figure 1: The decay rate is a decreasing function of bar length. We will accomplish this by composing 3 simple functions within a single m-file. The m-file (called cooldrive.m) will look like function cooldrive()% this is the driver % set a, t and a range of Land b and find i % and plot 12 against L end 1 2 3 4 5 6 7 8 9 10 11 12 function [x, iter) = debis (a,b,t,L) % for a given a, b, t, and I find : % code the bisection method here end function val - coolfun (x,L) %for a given and evaluate "cool" val = sin(x*L) + x*cos(x*L); end 1 In cooldrive I would set a = 0.1 and b = 3 and t = 0.01 (this is the tolerance) and compute the root x at each L = 1:0.1:4 and produce a figure like the one above. I recommend accumulating the L and x values and issuing one plot command at the end of the loop. For example, L = 1 : 0.1 : 4; 2 for cnt = 1:length (L) 3 (cnt) = debis (a,b,t,L(cnt)); end plot (L, X. 2) The trouble with this loop however is that () may have more than one root between a = 0.1 and b = 3. Because of this, it may be a good idea to adjust one or both of the endpoints of [a, b] as you change L. Specifically, as L increases, it is a good idea to let b decrease. You 4 5