PROGRAM LANGUAGE MUST BE C!

Program Numerical Integration

Introduction

For this program, lets explore some of the ways we can use C to perform numerical integration. Well restrict our attention to definite integrals on smooth curves only and look at two methods, called the rectangle rule and the trapezoidal rule respectively

(http://en.wikipedia.org/wiki/Numerical_integration).

With the rectangle rule, if we wish to calculate the area under a curve between two end points, a and b, we can evaluate the function at the midpoint between a and b and use that value to create a rectangle whose area will approximate the area under the curve between a and b. A diagram follows:

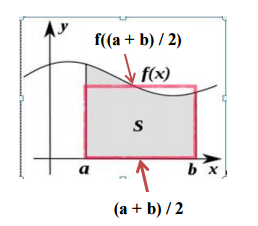
Here, the area of the red rectangle is consider an approximation for the definite integral between a and b. This area can be expressed by the following equation:

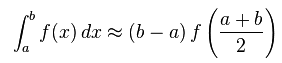
When this technique is applied to a larger region of the curve, we can divide the whole large region into smaller sub-regions of equal size, and apply the rectangle rule to each one. We may get something like the following:

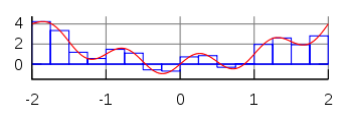
An approximation for the definite integral between, say, -2 and 2, in this case, will then be the sum of the areas of the rectangles. That sum will produce an approximation for the integral over the entire region.

With the trapezoidal rule, we can do something similar. The difference is that trapezoids instead of rectangles are used to create the underlying approximation. Here is a diagram:

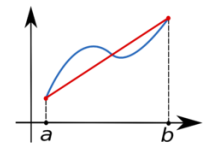
The area of the trapezoid (and therefore an approximation of the area under the curve) is given by the following equation:

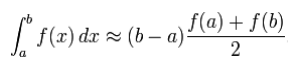
When applied to a larger region that is divided into many sub-regions, we get something like:

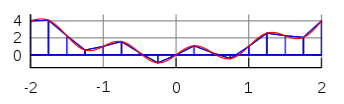
Here the technique is very similar: We divide the total region to be integrated into smaller subregions of equal size, calculate area of the trapezoid for each region, and then sum them all up to produce an approximation for the whole integral.

Assignment

Lets write a C program that will calculate an approximate value for the definite integral of a curve using each of the two methods, the rectangle rule and the trapezoidal rule. Hopefully well be able to observe how the approximate value improves as we increase the number of subintervals (decrease the size of the sub-intervals).

Your program should have separate functions for: (a) the calculation of a single rectangle; (b) the calculation of a single trapezoid; and (c) the calculation of f(x) for some x.

Initial Settings and Specifications

For our initial values, lets let NUM_INTERVALS = 100, and f(x) = x3 - 3x2 + 2. A diagram of that curve is depicted below. There are several opportunities to integrate that curve within [~0.3, ~2.3]. Have the computer ask the user which method he would like to use to do the integration, i.e., rectangle or trapezoid, and then to specify the endpoints. Your program will then return the result of the integral approximation based on the indicated method.