Program using Python

Consider the integral

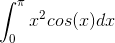
You are tasked with numerically determining the order of convergence for an integration method. Youll determine the order of convergence for each method by following these steps: (a) Calculate the integral with the given method for the following values of N subintervals:

N = 4, 16, 32, 64, 128, 256

For each value of N calculate the value of the integral, the error, and the value of h. Your results for each value of N should be printed in a table. Store your error values and values of h in two different arrays. (b) Plot the error values versus the value of h on a log-log plot (use plt.loglog(x, y)). Also on the log-log plot include line h versus h k . Vary the value of k until this second line matches the slope of the error line. This value of k is the order of convergence for your method. Note: this method will be similar to that of the last problem in the final project! Problem

3. Perform the above described steps for the composite trapezoid rule. Problem

4. Perform the above described steps for the composite Simpsons rule.

Given:

def compSimpson(f,a,b,n): h =(b-a) Seven = 0 Sodd = 0 S = 0 for j in range (2,n, 2): Seven =Seven + f(a + j*h) for j in range ( 1, n, 2): Sodd = Sodd + f(a + j*h) S = (h/3)*(f(a) + 2*Seven+4*Sodd+f(b)) Val = S return Val

def comptrap(f,a,b,n): h =(b-a) S = 0 for k in range (1,n): S += f(a + k*h) val = (h/2)*( f(a) + 2*S + f(b)) return val

def f(x): return x**2*np.cos(x)

def I(x): return (x**2 - 2)* np.sin(x) + 2 * x * np.cos(x)

2 cos(r)dr