Programming in MATLAB

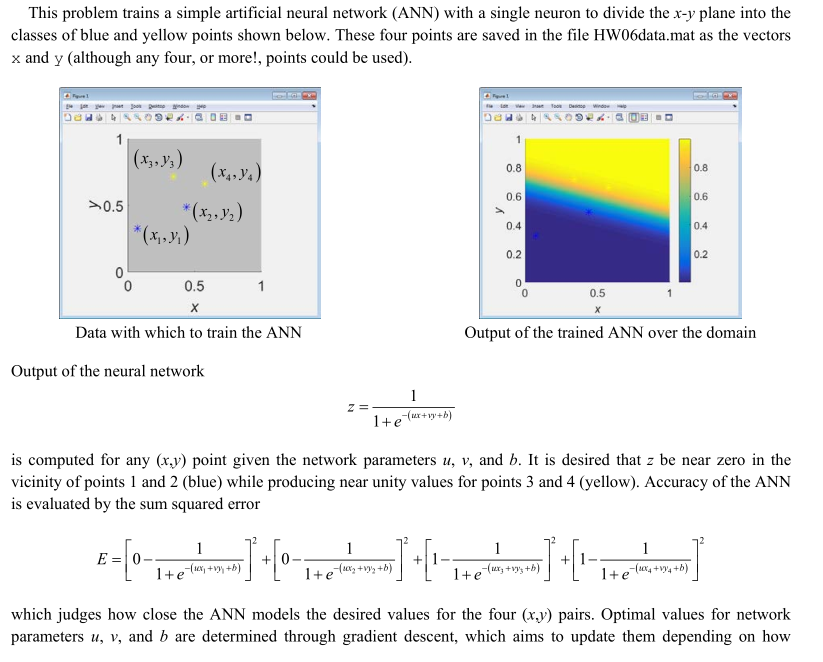
This problem trains a simple artificial neural network (ANN) with a single neuron to divide the x-y plane into the classes of blue and yellow points shown below. These four points are saved in the file HW06data.mat as the vectors x and y (although any four, or more!, points could be used) 0.8 0.8 x4,y4 0.6 0.6 0.5 r. 0.4 0.4 (x,yi) 0.2 0.2 0.5 0 0.5 Data with which to train the ANN Output of the trained ANN over the domain Output of the neural network 1+b) is computed for any (x.y) point given the network parameters u, v, and b. It is desired that z be near zero in the vicinity of points 1 and 2 (blue) while producing near unity values for points 3 and 4 (yellow). Accuracy of the ANN is evaluated by the sum squared error 1 tb) +4+b) which judges how close the ANN models the desired values for the four (xy) pairs. Optimal values for network parameters u, v, and b are determined through gradient descent, which aims to update them depending on how This problem trains a simple artificial neural network (ANN) with a single neuron to divide the x-y plane into the classes of blue and yellow points shown below. These four points are saved in the file HW06data.mat as the vectors x and y (although any four, or more!, points could be used) 0.8 0.8 x4,y4 0.6 0.6 0.5 r. 0.4 0.4 (x,yi) 0.2 0.2 0.5 0 0.5 Data with which to train the ANN Output of the trained ANN over the domain Output of the neural network 1+b) is computed for any (x.y) point given the network parameters u, v, and b. It is desired that z be near zero in the vicinity of points 1 and 2 (blue) while producing near unity values for points 3 and 4 (yellow). Accuracy of the ANN is evaluated by the sum squared error 1 tb) +4+b) which judges how close the ANN models the desired values for the four (xy) pairs. Optimal values for network parameters u, v, and b are determined through gradient descent, which aims to update them depending on how