Projectile Motion Concept Question

I have a question about the Specific

"Time of flight" formula for Projectile Motion

*As well as incorporating other formulas in order to consolidate and make a holistic review on the formulas and their derivation from the motion equations for projectile motion and its various questions

Source 1 from Lecture:

Time of flight = Square root of 2* Height / g , derived from the motion equation of y= 1/2gt^2

Should it be -1/2gt^2 given gravitational acceleration downwards?

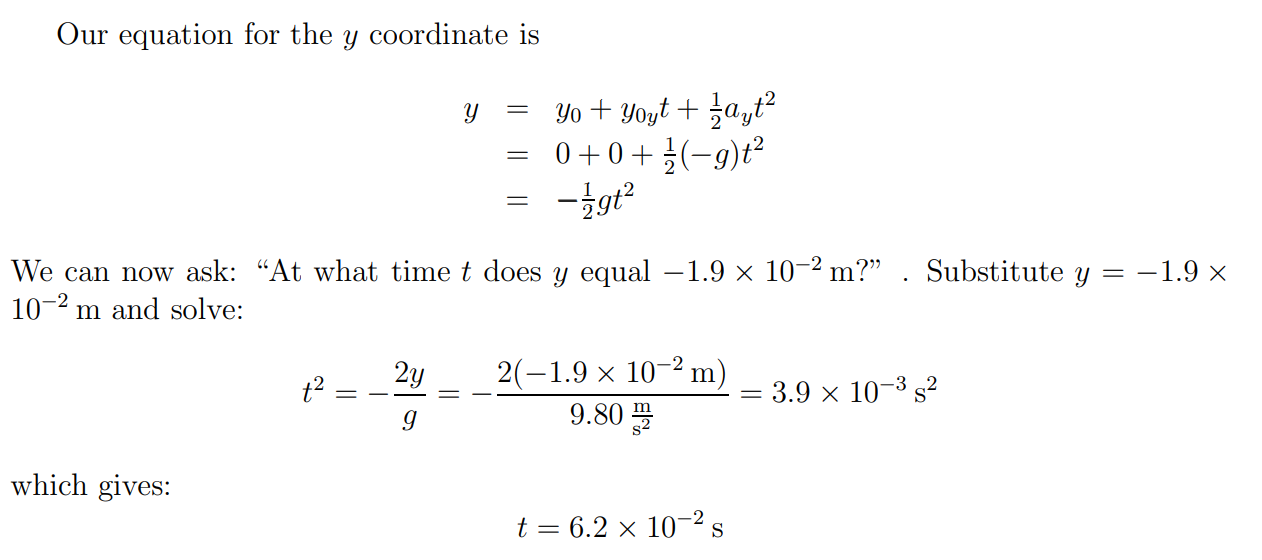
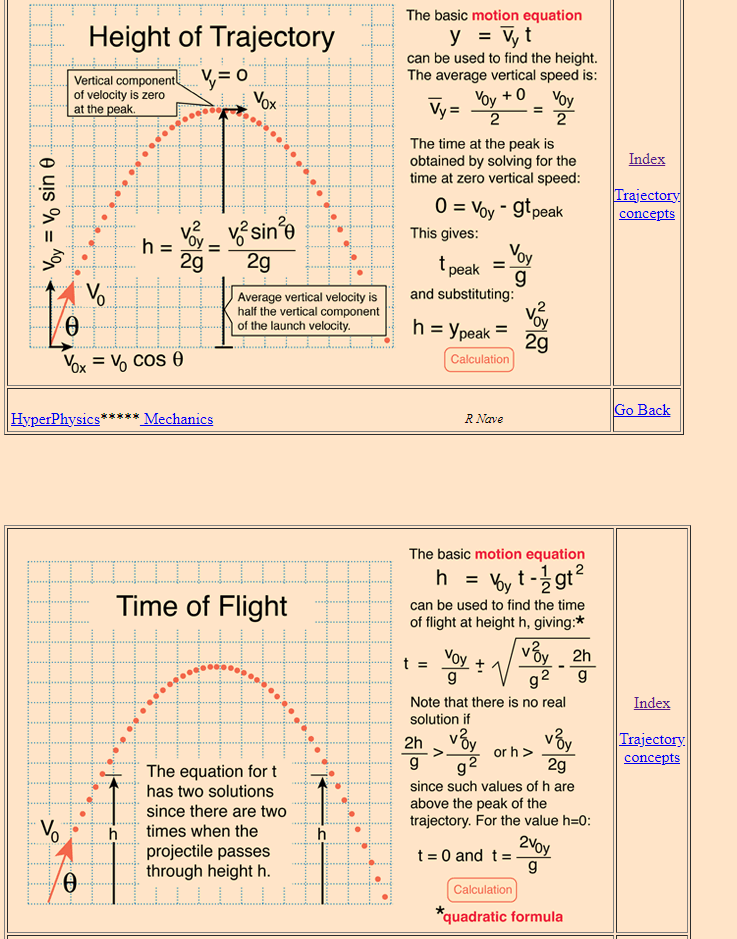
Horizontal D= V ramp flight VEV ramp = constant Vertical 2 H H=- 9 t night SO t flight v=gt flight V=1 + V XOur equation for the y coordinate is y : to + yOyt + $th = 0 + 0 + ;(g):2 = 9152 We can now ask: \"At What time it does 3,: equal 1.9 X 102 In?\" . Substitute y = 1.9 X 102 m and solve: _ ,2 _2_y = _2( 1.9 x 10 m) = 3.9 X10432 g 9.80% 92 which gives: 1': 6.2 X 102 s Projectile motion . Projectile refers to an object that is in flight along the horizontal and vertical direction simultaneously. . Acceleration acts only in the vertical direction due to acceleration due to gravity (g). . No acceleration in the horizontal direction. usin 0 B . Projectile motion is always in the form of parabola. U U cos 0 g y = ax + bx A U COS 6 C Formulas for projectile motion Components of velocity at time t u, = u cose u, = u sine-gt Position at time t x = (u cos0)t y = (u sin0)t - 1/2 gt? Equation of path of projectile motion y = (tan 0)x - gx /2(u cose)? Time of maximum height to = u sine /g Time of flight 2tm = 2(u sin0/g) Maximum height of projectile hm = (u sin0)?/2g Horizontal range of projectile R = u' sin 20/g Maximum horizontal range ( 0. = 45* ) Rm = u'/gThe basic motion equation Height of Trajectory y = Wt can be used to find the height. Vertical component V= 0 The average vertical speed is: of velocity is zero Vox. at the peak. Vy= Voy + 0 Voy 2 2 The time at the peak is obtained by solving for the Index time at zero vertical speed: Trajectory You = Vo Sin 0 0 = Voy - 9tpeak concepts v2sin'0 This gives: h = Voy = 2g 2g t peak = Voy g " Vo Average vertical velocity is and substituting: half the vertical component of the launch velocity. h = ypeak = Yoy 29 Vox = Vo COS 0 Calculation R Nave Go Back HyperPhysics* * * * * Mechanics The basic motion equation h = by t- gt2 Time of Flight can be used to find the time of flight at height h, giving:* 1 = Voy + vBy 2h g g2 9 Note that there is no real Index solution if 2h Voy or h > vBy Trajectory. concepts The equation for t g 2g has two solutions since such values of h are since there are two above the peak of the trajectory. For the value h=0: times when the projectile passes t = 0 and t= 2voy through height h. g Calculation *quadratic formula