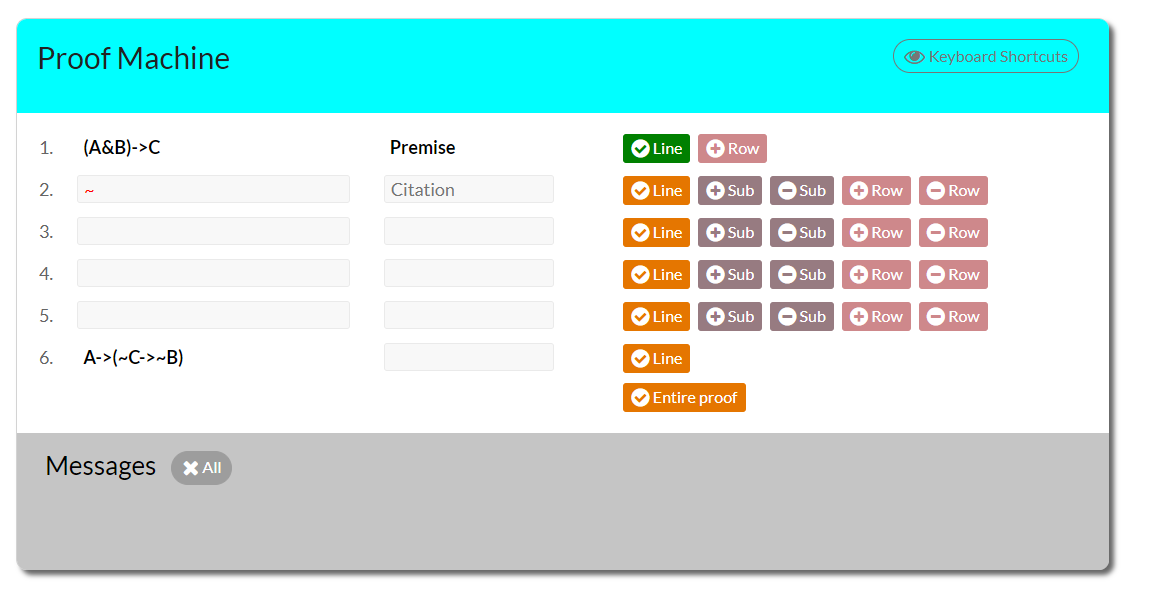
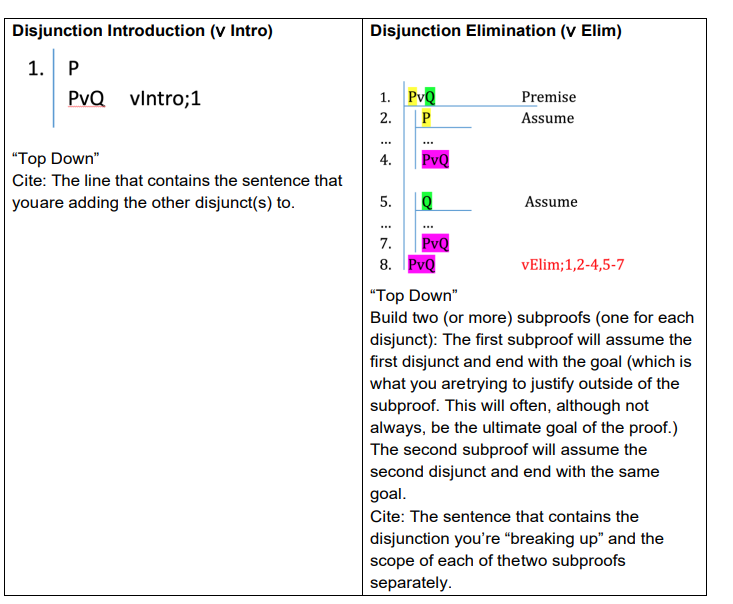
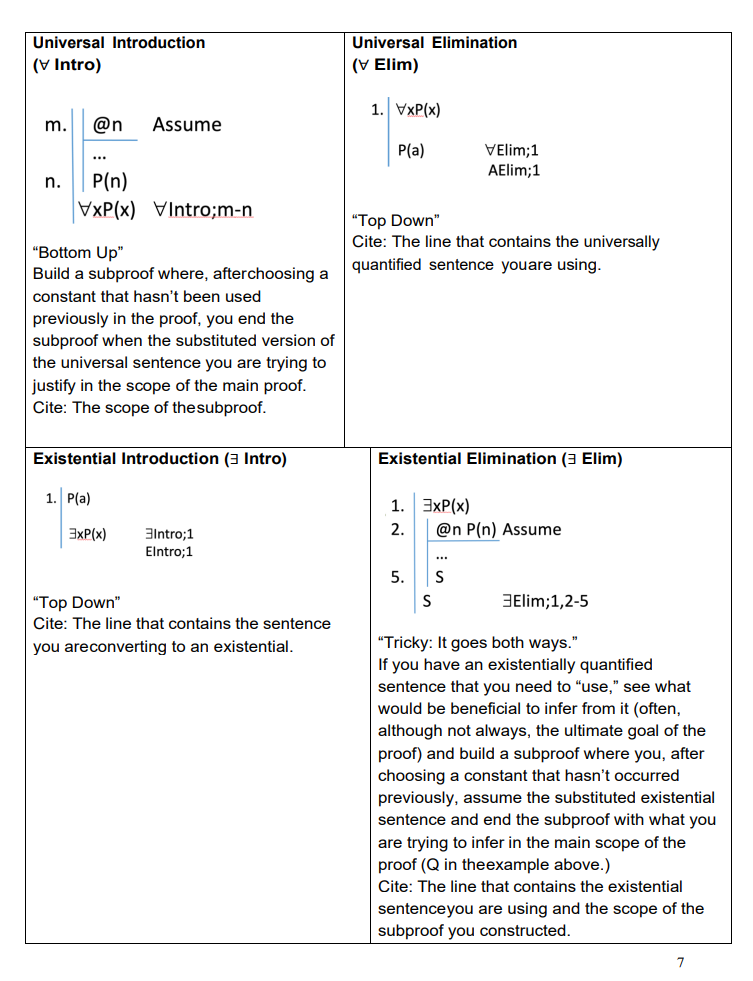
Proof Machine OKeyboard Shortcuts 1. (A&B)->C Premise Line + Row 2. Citation Line + Sub - Sub + Row Row 3. Line + Sub - Sub + Row - Row 4. Line + Sub Sub + Row Row 5. Line + Sub - Sub + Row - Row 6. A->(~C->~B) Line Entire proof Messages * AllIdentity Introduction (= Intro) Identity Elimination (= Elim) P(n) on=n =Intro n = m "Top Down" D P(m) =Elim;1,2 Cite: No "Top Down" citation Cite: The line that contains the identity expression and the line that you are "swapping in" (in this caseP(n).) Conjunction Introduction (& Intro) Conjunction Elimination (& Elim) 1. P 1. P&Q P & Elim;1 2. Q P&Q &Intro;1,2 "Top Down" "Top Down" Cite: The line that contains the Conjunction. Cite: The lines that contain the sentences you areconjoining together.Disjunction Introduction (V Intro) Disjunction Elimination (V Elim) 1. P PvQ vintro;1 1. PvQ Premise 2. P Assume "Top Down" 4. PVQ Cite: The line that contains the sentence that youare adding the other disjunct(s) to. 5 O Assume 7 PvQ 8. PvQ vElim;1,2-4,5-7 "Top Down" Build two (or more) subproofs (one for each disjunct): The first subproof will assume the first disjunct and end with the goal (which is what you aretrying to justify outside of the subproof. This will often, although not always, be the ultimate goal of the proof.) The second subproof will assume the second disjunct and end with the same goal. Cite: The sentence that contains the disjunction you're "breaking up" and the scope of each of thetwo subproofs separately.Negation Introduction (~ Intro) ~Intro:n-m \"'Bottom Up\"" Build a subproof where you assume the 'opposite\"of the sentence (in the example ~F) and end the subproof with a contradiction. Cite: The scope of the subproof. Note: You can use this strateqgy to introduce P intothe main proof if you take advantage of the fact that P = ~~P 1 Introduction (L Intro) 1.1 Q 2. | ~Q # #Intro:1,2 \"Top Down\" Cite: The two lines that demonstrate thecontradiction. Negation Elimination (- Elim) This simple rule allows us to eliminate \"doublenegations.\" ~Elim;1 \"Top Down"\" Cite: The line that contains the double negation. 1 Elimination (L Elim) 1. | # R #Elim;1 \"Top Down\" Cite: The line that contains the #. Note: # Elim allows you to use the # to put anythingyou want into the proof, as long as it's within the same scope line. Conditional Elim (-> Elim) Conditional Intro (-> Intro) 1. P->Q 2. P P Assume Q ->Elim;1,2 ... ... 3. P->Q -Intro;1-3 "Top Down" Cite: The line that contains the Conditional and the line that "Bottom Up" contains theantecedent. Build a subproof where you assume the antecedentand end with the consequent. Cite: The scope of the subproof. Biconditional Elimination ( Elim) Biconditional Introduction ( Intro) 1. 1. P Assume 2. P .. Q Elim;1,2 3. Q [NOTE: OR] 4. Q Q Assume 4. Elim;1,4 6. P "Top Down" PQ Intro;1-3,4-6 Cite: The line that contains the Biconditional and the line that contains the "Bottom Up" "other" term. Build two separate subproofs: one that assume the antecedent and ends with the consequent and the other that assumes the consequent and ends with the antecedent. Cite: The scope of each subproof separately.Universal Introduction Universal Elimination (onuj A) (WII3 A) ( X) dx A T m. @n Assume P(a) T:WII3 A AElim;1 n. P(n) u-w:onujA (x)dxA "Top Down" "Bottom Up" Cite: The line that contains the universally Build a subproof where, afterchoosing a quantified sentence youare using. constant that hasn't been used previously in the proof, you end the subproof when the substituted version of the universal sentence you are trying to justify in the scope of the main proof. Cite: The scope of thesubproof. Existential Introduction (3 Intro) Existential Elimination (3 Elim) 1. P(a) 1. 3xP(x) 3xp (x) 3Intro;1 2. @n P(n) Assume Elntro;1 5 "Top Down" S 3Elim;1,2-5 Cite: The line that contains the sentence you areconverting to an existential. "Tricky: It goes both ways." If you have an existentially quantified sentence that you need to "use," see what would be beneficial to infer from it (often, although not always, the ultimate goal of the proof) and build a subproof where you, after choosing a constant that hasn't occurred previously, assume the substituted existential sentence and end the subproof with what you are trying to infer in the main scope of the proof (Q in theexample above.) Cite: The line that contains the existential sentenceyou are using and the scope of the subproof you constructed