Question: Prove that Theorem 13.1 (vi) using the simple ftn, nonnegative ftn and general ftn. (vi) If X is measurable in N and E(|XY|) <

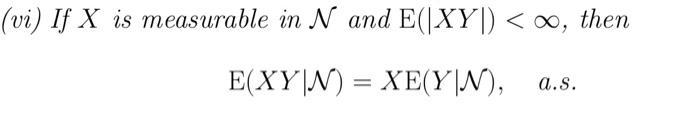
Prove that Theorem 13.1 (vi) using the simple ftn, nonnegative ftn and

general ftn. (vi) If X is measurable in N and E(|XY|) <

Prove that Theorem 13.1 (vi) using the simple ftn, nonnegative ftn and general ftn. (vi) If X is measurable in N and E(|XY|) < , then E(XY|N) = XE(Y|N), a.s.

Step by Step Solution

★★★★★

3.43 Rating (172 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Document Format (2 attachments)

63676b193787d_234367.pdf

180 KBs PDF File

63676b193787d_234367.docx

120 KBs Word File

Students Have Also Explored These Related Mathematics Questions!

In Theorem 3.37, prove that if p i = p j , then we cannot determine whether an error occurs in the ith or the jth component of the received vector. (Throughout this proof we denote by ai the ith...

In Theorem 3.37, prove that if B = A, then PGx = 0 for every x in Z k 2 . (Throughout this proof we denote by ai the ith column of a matrix A.) With P and G as in the statement of the theorem, assume...

Using Theorem 7.10 or Theorem 9.30, prove that each of the following limits exists. Find a value for the limit in each case. a) b) where f is continuously differentiable on [0, 1] and f'(0) > 0. c)...

1. Sketch the function f(x) = 2x+ 1 if x #1 5 if x = 1 2. What is lim f(x) from question 1? 3. Prove that lim (2x + 1) =3 using the 6 - & definition. Sec 1.3 Find the limits: 4. lim (-x2 + 3) X-+1 5....

2.42 The cantilever beam shown has a rectangular cross section b 2c. (a) Using the equation , = -My/1,, prove that a, = wxy/(611). (b) Determine (x, y) and or,(x, y) using Eqs. (2.4-2). (c) Show...

Question 4 (4 points) a) Give an example of an odd function and prove that it is odd. b) Using the same function from (a) and your knowledge of transformations, apply at least two that would change...

1 MATHEMATICS Find the centre and radius of the circle formed by all the points represented by z x iy satisfyin k k 1 where a and are constant complex numbers given b the relation z BI a a B B iB 2...

Lab 13: Waves & interference Learning Objectives Differentiate between types of waves. Understand how to mathematically describe traveling waves. Understand how to model the propagation of a pulse on...

Find the solution to the following questions. 1. If p is the probability of 'successes' at a single trial, obtain the probability of r 'successes' out of n independent trials. 2. Discuss the nature...

Question: Assume you have two boxes An and B. Box A contains 7 dark marbles, 4 white marbles. Box B contains 7 white and 4 dark marbles. An arbitrary test is acted in two consecutive preliminaries by...

An organization's failure to fulfill its contractual obligations could have legal consequences. Group of answer choices True False

ABC Company reports their earnings and expenses data from the years 2004 to 2018 as shown in the table. Use Linear Forecasting and regression to calculate the expense value in the year 2021. Years...

The term COCOA, according to the author, best fits within the concept of area analysis and is generally considered within : Group of answer choices Military Missions Cultural Geography and Strategic...

Problem 6-18 (Algo) Relevant Cost Analysis in a Variety of Situations [LOG-2, LOG-3, LOG-4] Andretti Company has a single product called a Dak. The company normally produces and sells 87,000 Daks...

Sweet Memories Inc (for Q11-13) Sweet Memories Inc is a company that produces Customized Family Portraits. Preparing a Family Portrait involves 3-steps: Collect the Images and Stories, Edit, and...

Rebecca v My Home Courses Catalog and Study Tools Rental Options College Success Tips Career Success Tips Help Give Feedback H ng.cengageicom a MindTap - Cengage Learning '2: CENGAGE | MINDTAP...

r RF = 5%; r M = 10%; RP M = 5%, and beta = 1.1 What is WCE's required rate of return? Do not round intermediate calculations. Round your answer to two decimal places. % If inflation increases by 3%...

Controls can be identified based on their function. The functions are preventive, detective, and corrective. A. True B. False

The trace of a square matrix A is the sum of the diagonal entries in A and is denoted by tr A. It can be verified that tr(FG) = tr(GF) for any two n x n matrices F and G. Show that if A and B are...

An affine transformation T: has the form T(x) = Ax + b, with A an m ( n matrix and b in. Show that T is not a linear transformation when b ( 0. (Affine transformations are important in computer...

The circuit in the figure is described by the equation where iL is the current through the inductor L and vC is the voltage drop across the capacitor C. Find formulas for iL and vC when R = .5 ohm, C...

The United Nations Development Programme (UNDP) uses the Human Development Index (HDI) in an attempt to summarize in one number the progress in health, education, and economics of a country. In 2012,...

In justifying his choice of a model, a student wrote, "I know this is the correct model because R2 = 99.4%." a) Is this reasoning correct? Explain. b) Does this model allow the student to make...

The researcher in Exercise 9 is content with the second regression. But he has found a number of shells that have large residuals and is considering removing all them. Is this good practice?