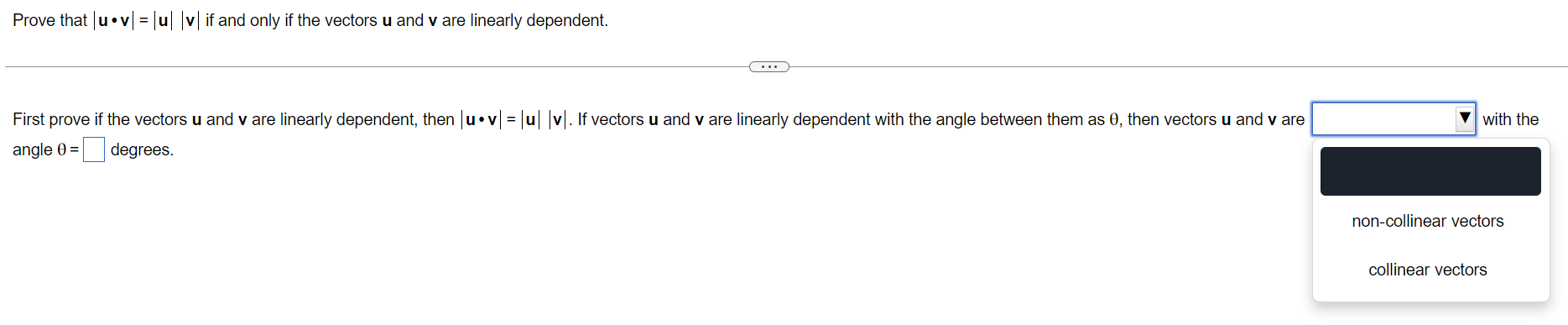
Prove that | u . v| = |u| |v| if and only if the vectors u and v are linearly dependent. First prove if the vectors u and v are linearly dependent, then |u . v| = u| |v|. If vectors u and v are linearly dependent with the angle between them as 0, then vectors u and v are with the angle 0 = degrees. non-collinear vectors collinear vectors