Question: Prove the following statements using Structural Induction. Polynomials f(x) can be defined recursively as follows: 1 and x are polynomials If p and q are

Prove the following statements using Structural Induction.

Polynomials f(x) can be defined recursively as follows:

Prove the following statements using Structural Induction. Polynomials f(x) can be defined 1 and x are polynomials

recursively as follows: 1 and x are polynomials If p and q If p and q are polynomials, so are p + q, p are polynomials, so are p + q, p 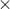q, cp, where c q, cp, where c is a constant.

Prove that the polynomials defined as above can be expressed as

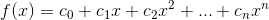
is a constant. Prove that the polynomials defined as above can be

where, expressed as where, 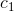, i N, are constant coefficients., i image text in transcribed N, are constant coefficients.

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

Q:

Prove the following statement using Structural Induction. The set S is defined recursively as follows: 3 S If x S and y S, then x + y S Prove that S is the set of all positive integers that are...

Q:

2. (20 points) Prove the following statements using Strong Induction. (a) A postage of n cents can be formed using just 4 and 7 cent stamps. (b) A sequence an is defined recursively as follows: n=1...

Q:

1: Refinancing a loan. Suppose someone takes out a home improvement loan for $30,000. The annual interest on the loan is 6% and is compounded monthly. The monthly payment is $600. Let an denote the...

Q:

In a Hopfield neural network configured as an associative memory, with all of its weights trained and fixed, what three possible behaviours may occur over time in configuration space as the net...

Q:

When studying modular arithmetic, we made the claim that, if we replace a variable in an arithmetic expression with a value that it is congruent to, the resulting expression will be congruent to the...

Q:

Assessment The following question was given to ChatGPT. However, it was later learned that this should not be provable Determine what's correct, what's incorrect, give a counterexample that shows it...

Q:

Problem 2. The recursive data type, binary-2PTG, of binary trees with leaf labels, L, is defined recursively as follows: e Base case: (leaf; l) e binary-2PTG, for all labels 1 EL. e Constructor case:...

Q:

Orthogonality and least squares Problem 8.10 (Optional). Assume n is a power-of-2 (i.e., n = 2* for some non-negative integer k). The nxn Hadamard matrix Hn is defined recursively as follows: H1 =...

Q:

In many applications in CS, we need to convert things (eg, proofs or programs) into a standard or "normal form that has the same meaning as the original. For example it's easier to build a parser or...

Q:

prove using induction please (a) A set of strings L (over alphabet sigma = {0, 1}) is defined recursively as follows: the empty string epsilon elementof L, and for all strings x, y elementof L, 1x0y1...

Q:

For each of the drop down menus, choose the answer that makes the following statement correct. For firms in perfectly (purely) competitive markets, long run economic profits are: select answer...

Q:

In a Time/Money Magazine poll of Americans of age 18 years and older, 65% agreed with the statement, We are less sure our children will achieve the American Dream (Time, October 10, 2011). Assume...

Q:

Hene s i n 8 = 0 Suppose the price of a share of Google stock is $ 5 0 0 . An April calt option on Google stock has a premturn of ss and un wantion price of $ 5 0 0 . Ignoring commissions, the holder...

Q:

Subject - Marketing Management Case Analysis Bharti Airtel is in discussions with smartphone contract manufacturers in India to develop low- cost 4G devices which could be sold either under the...

Q:

Explain the purpose of the Project Charter and its relationship to Management Approval for a Project.

Q:

What is Change Control and how does it operate?

Q:

How do Data Requirements relate to Functional Requirements?