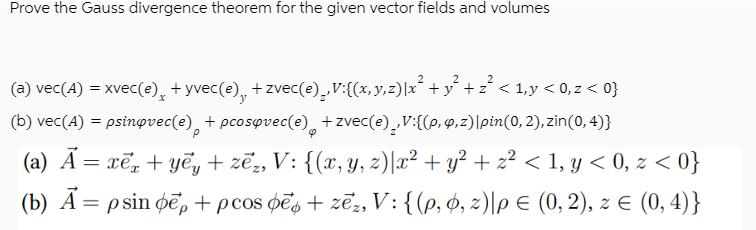
Prove the Gauss divergence theorem for the given vector fields and volumes (a) vec(4) = xvec(e)x + yvec(e),, + zvec(e) ,V:{(x, y, z)|x + y + z < 1,y < 0, z < 0} (b) vec(A) = psinovec(e) + pcosovec(e) + zvec(e),,V:{(p,q,z)|pin(0, 2), zin(0, 4)} P (a) A = xex + y + z, V: {(x, y, z)|x + y + z < 1, y < 0, z < 0} (b) A = psin e + pcos de + z, V: {(p, o, z)|p = (0, 2), z = (0, 4)}