Question: Prove the geometric series formula Use this to explain why P is really 1 1-2 = 1+x+x + k=0 ak k X

Prove the geometric series formula

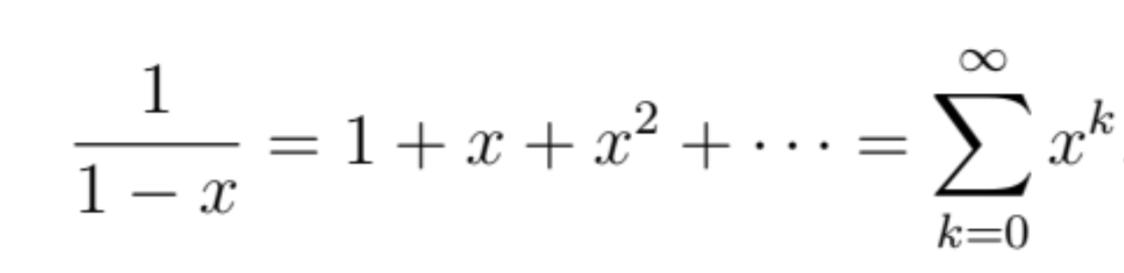
( frac{1}{1-x}=1+x+x^{2}+cdots=sum_{k=0}^{infty} x^{k} )

Use this to explain why P is really

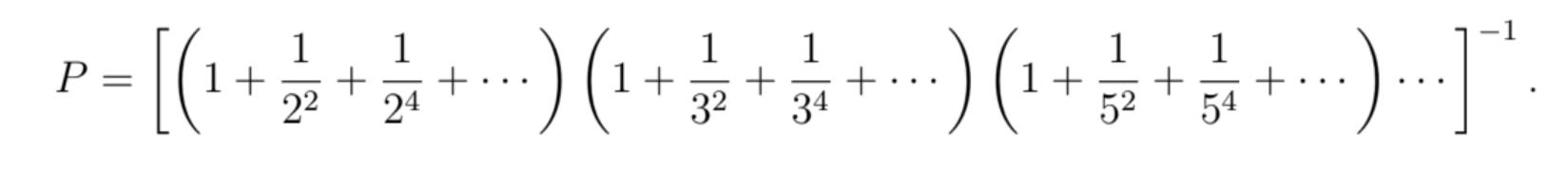
( P=left[left(1+frac{1}{2^{2}}+frac{1}{2^{4}}+cdotsight)left(1+frac{1}{3^{2}}+frac{1}{3^{4}}+cdotsight)left(1+

1 1-2 = 1+x+x + k=0 ak k X

Step by Step Solution

★★★★★

3.50 Rating (153 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

aAnsThe expression 11x can be expanded into a geometric series as follows 11x1xx2x3mathrmno To see w... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Q:

The beam consists of two segments pin connected at B. Draw the shear and moment diagrams for thebeam. 700 Ib 150 lb/ft 800 Ib - ft IB -8 ft- -6 ft-

Q:

KYC's stock price can go up by 15 percent every year, or down by 10 percent. Both outcomes are equally likely. The risk free rate is 5 percent, and the current stock price of KYC is 100. (a) Price a...

Q:

In the Household Expenditure Statistics: Year Ended 30 June 2016 (Statistics New Zealand, , licensed by Statistics New Zealand for re-use under the Creative Commons Attribution 3.0 New Zealand...

Q:

The difference map : Cn Cn is defined as = S - I, where S is the shift map of Exercise 8.2.13. (a) Write down the matrix corresponding to A. (b) Prove that the sampled exponential vectors w0,...

Q:

The sales are $10 million this and expected to grow at 5% in real terms for the next three years. The appropriate nominal discount rate is 10%. The inflation is expected to be 2% per year during the...

Q:

now//You are asked to price some options on KYC stock. KYC's stock price can go up by 15 percent every year, or down by 10 percent. Both outcomes are equally likely. The risk free rate is 5 percent,...

Q:

Please explain it in details, thanks. In this exercise we will derive the formulas for the present value and future value of an ordinary annuity. Suppose there are N pe- riods and that today, time t...

Q:

i) Life insurance premium A life insurance policy is a financial contract that collects a premium of p per period from the insured and pays out a lump sum benefit upon the death of the insured. Let m...

Q:

1. Computing mortgage payments and balances Suppose you borrow L dollars, which you are to repay over a period of 20 years at 6% interest, compounded monthly. How much will your monthly payments be?...

Q:

1. Computing mortgage payments and balances Suppose you borrow L dollars, which you are to repay over a period of 20 years at 6% interest, compounded monthly. How much will your monthly payments be?...

Q:

MAS183 Statistical Data Analysis 1 Project Description " give 2 examples for this question so that i can choose one question for my assignment" "THIS IS THE ACTUAL QUESTION PROVIDE ME WITH ATLEAST 2...

Q:

A steel truss is shown in Figure Q1b. Assuming that the same steel section is used for all members: Calculate the area of the the smallest steel section such that the maximum vertical deflection at...

Q:

Describe the primary conflict of interest that caused the public accounting industry to fail in its duty to protect the investing publics interests in the 1990s.

Q:

35. It is not the case that both Iran gives up its nuclear program and Syria or Pakistan combats terrorism. Translate the following statements into symbolic form using capital letters to represent...

Q:

Preston Enterprises uses the direct write-off method of accounting for uncollectible accounts. On October 12, a very large account was written off. The amount was subsequently recovered on December...

Q:

The 2018 income statement and comparative balance sheet of Rolling Hills, Inc. follow: Additionally, Rolling Hills purchased land of $21,100 by financing it 100% with long-term notes payable during...

Q:

As newlywed, John and Beth are considering their short-term and long term personal financial plan. If you were hired to give them advice, what specific goals and plan of action would you help them...

Q:

The income statement of Boost Plus, Inc. follows: Additional data follow: a. Acquisition of plant assets is $124,000. Of this amount, $108,000 is paid in cash and $16,000 by signing a note payable....

Q:

The records of Vintage Color Engraving reveal the following: Compute cash flows from operating activities by the indirect method for year ended December 31, 2018. Net income Sales revenue Loss on...

Q:

Ethics in advertising suggest that an activity the organization undertakesMultiple Choicemust abide by the law but may stil be within the First Amendment, freedom of speech.should always be generous...

Q:

Determine the magnitude of the resultant force F R = F 1 + F 2 and its direction, measured clockwise from the positive u axis. A F 30 45 C

Q:

The man tries to open the valve by applying the couple of forces of F = 75 N to the wheel. Determine the couple of moment produced. F -150 mm-150 mm- F

Q:

Determine the force P that must be applied to the handle of the lever so that the wheel is on the verge of turning if M = 300 N m. The coefficient of static friction between the belt and the wheel...

Q:

Questions 1. Identify the steps of the product design process used by Harveys. (Specifically, consider market analysis, concept development, prototype development, and (external) testing and...

Q:

In 2002 Wilson Sporting Goods wanted to enter the market for youth baseball batting helmets with a durable, strong, stylish youth batting helmet with improved ventilation and a quick and simple...

Q:

In 2004 Calor (T-Fal), a member of Groupe SEB of France, worlds largest kitchen products and small appliances manufacturer, commissioned the product design firm of SeymourPowel to redesign its mid...