Question: Prove the given theorem and provide (1) examples. Theorem 1.5 (Mean - value theorem for derivatives) If f (x) is continuous in [a, b] and

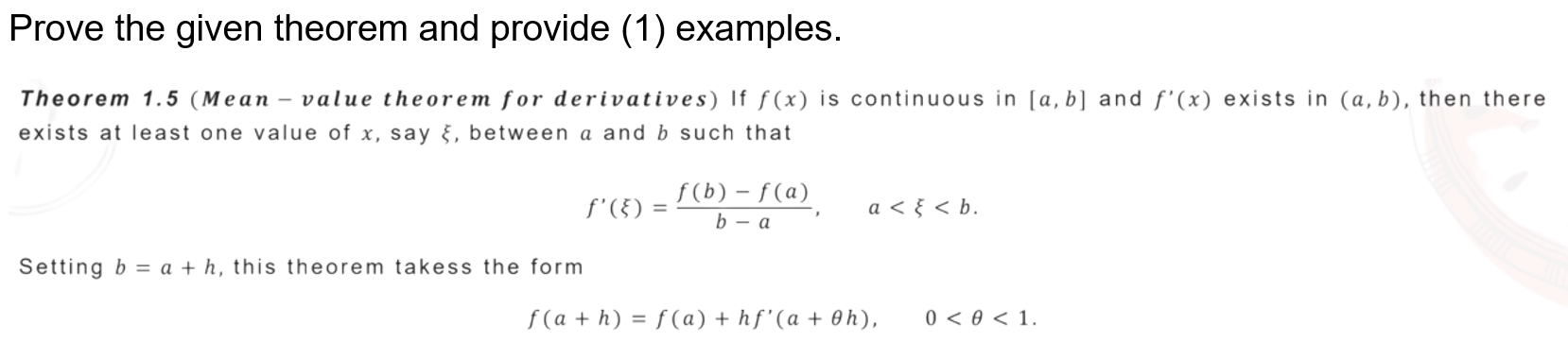
b] and f'(x) exists in (a, b), then there exists at least

one value of x, say , between a and b such that

Prove the given theorem and provide (1) examples. Theorem 1.5 (Mean - value theorem for derivatives) If f (x) is continuous in [a, b] and f'(x) exists in (a, b), then there exists at least one value of x, say , between a and b such that f' (5) = 1(b) - f(a) a

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Help me with that 8. . [0/1.42 Points] DETAILS PREVIOUS ANSWERS SCALC9 3.2.013. MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER Consider the following function. RX) = 1 - x2/3 Find R(-1) and f( 1 ) . R( -...

8. [0.5/1 Points] DETAILS PREVIOUS ANSWERS SCALC8 3.2.505.XP. MY NOTES PRACTICE ANOTHE Does the function satisfy the hypotheses of the Mean Value Theorem on the given interval? f ( x ) = - X x + 9'...

Does the function satisfy the hypotheses of the Mean Value Theorem on the given interval? f ( x ) = X- x + 4 [1, 8] Yes, it does not matter if f is continuous or differentiable; every function...

5. [-/2 Points] DETAILS MY NOTES Does the function satisfy the hypotheses of the Mean Value Theorem on the given interval? f ( x ) = [1, 5] x Yes, it does not matter if f is continuous or...

5. [-/2 Points] DETAILS MY NOTE Does the function satisfy the hypotheses of the Mean Value Theorem on the given interval? f ( x ) = - x' [1, 5] Yes, it does not matter if f is continuous or...

1. [-/3 Points] DETAILS LARCALC9 3.2.005. Find the two x-intercepts of the function f and show that f '(x) = 0 at some point between the two x-intercepts. f( x ) = x2 - 2x - 15 ( x, y ) = ( (smaller...

1.) The absolute maximum of the function f ( x ) = 1 + x + x 2 x on the interval [-2, 2] is 1/2 at x = 1, and the absolute minimum is -1/2 at x = -1. For 2) and 3) the verification is in the...

2. [0/2 Points] DETAILS PREVIOUS ANSWERS LARCALCET7 4.R.015. MY NOTES Determine whether the Mean Value Theorem can be applied to f on the closed interval [a, b]. (Select all that apply.) f(x) = 14 -...

Determine whether the Mean Value Theorem can be applied to f on the closed interval [a, b]. (Select all that apply.) f ( x) = X [1, 4] x - 5' Yes, the Mean Value Theorem can be applied. O No, f is...

These are the practice problems for the final exam, the answers are there, I just want to know how to solve them? So can you please show to me the solving steps for each question! MATH 1720/1760...

On January 10 of the current year, Sydney transfers to Loretta Corporation a machine purchased three years ago for $97,000. On the transfer date, the machine has a $55,000 adjusted basis and a...

Assume that you just won the state lottery. Your prize can be taken either in the form of $40,000 at the end of each of the next 25 years (i.e., $1 million over 25 years) or as a lump sum of $500,000...

The interest rate at which the Federal Reserve Banks lend to commercial banks is called the Multiple Choice prime rate. short-term rate. discount rate. federal funds rate

(2) You are playing the computer game Civilization III designed by Sid Meir. In this game you are managing a medieval army. You are tasked with transporting soldiers from their 2 barracks to 3...

3. It is the commitment you show that is the deciding factor.

4. It is the principle of equality (according to very specific criteria of equality) that is crucial.

7. As your starting point, take a discussion you have had with a person at your workplace. Answer the following questions: Answer the following questions: What did you want to achieve? How did you...