Python

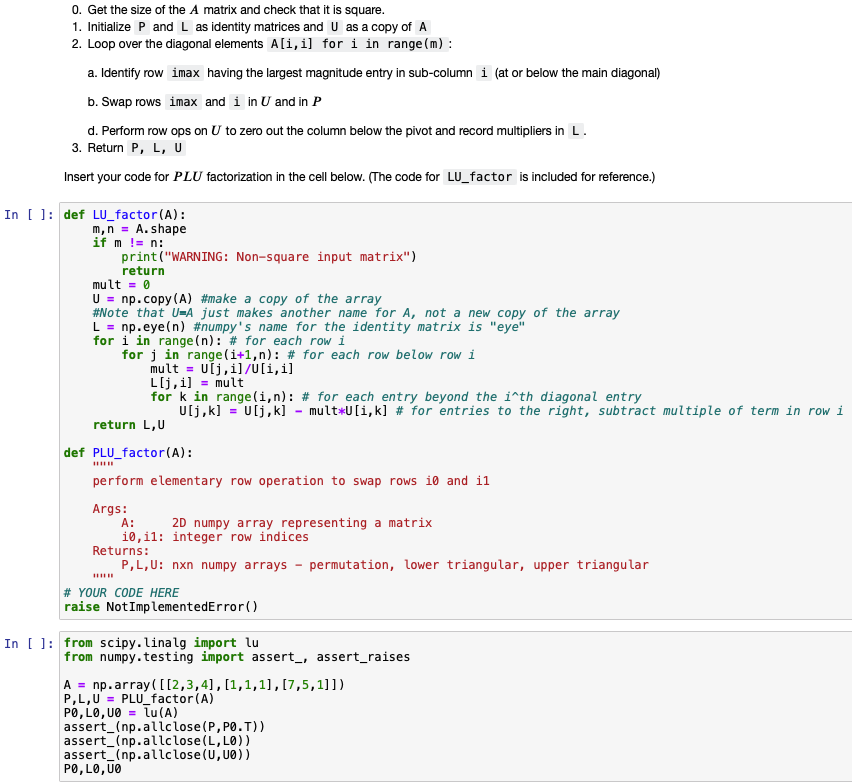
0. Get the size of the A matrix and check that it is square. 1. Initialize P and L as identity matrices and U as a copy of A 2. Loop over the diagonal elements A[i,i] for i in range(m): a. Identify row imax having the largest magnitude entry in sub-column i (at or below the main diagonal) b. Swap rows imax and i in U and in P d. Perform row ops on U to zero out the column below the pivot and record multipliers in L. 3. Return P, L, U Insert your code for PLU factorization in the cell below. (The code for LU_factor is included for reference.) In [ ]: def LU_factor(A): m, n = A. shape if m != n: print("WARNING: Non-square input matrix") return mult = 0 U = np.copy (A) #make a copy of the array #Note that U=A just makes another name for A, not a new copy of the array L = np.eye(n) #numpy's name for the identity matrix is "eye" for i in range(n): # for each row i for j in range(i+1,n): # for each row below row i mult = U[j,i]/U[i,i] L[j,i] = mult for k in range(i,n): # for each entry beyond the inth diagonal entry U[j,k] = U[j, k] - mult*U[i,k] # for entries to the right, subtract multiple of term in row i return L,U def PLU_factor(A): perform elementary row operation to swap rows io and il Args: A: 2D numpy array representing a matrix i0, il: integer row indices Returns: P,L,U: nxn numpy arrays permutation, lower triangular, upper triangular # YOUR CODE HERE raise Not ImplementedError() In [ ]: from scipy. linalg import lu from numpy.testing import assert_, assert_raises A = np.array( [[2,3,4],[1,1,1), 17,5,1]]) P,L,U = PLU_factor(A) PO, LO,00 = lu(A) assert_(np.allclose(P,PO.T)) assert_(np.allclose (L, LO)) assert_(np.allclose(0,00)) PO, LO,00