PYTHON CODE

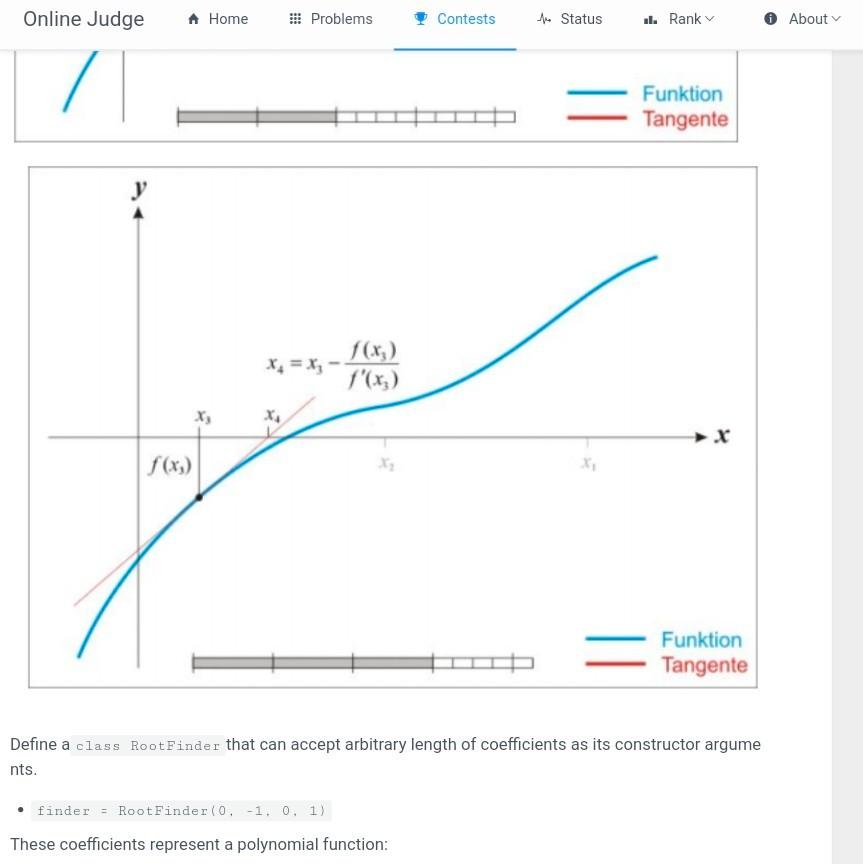
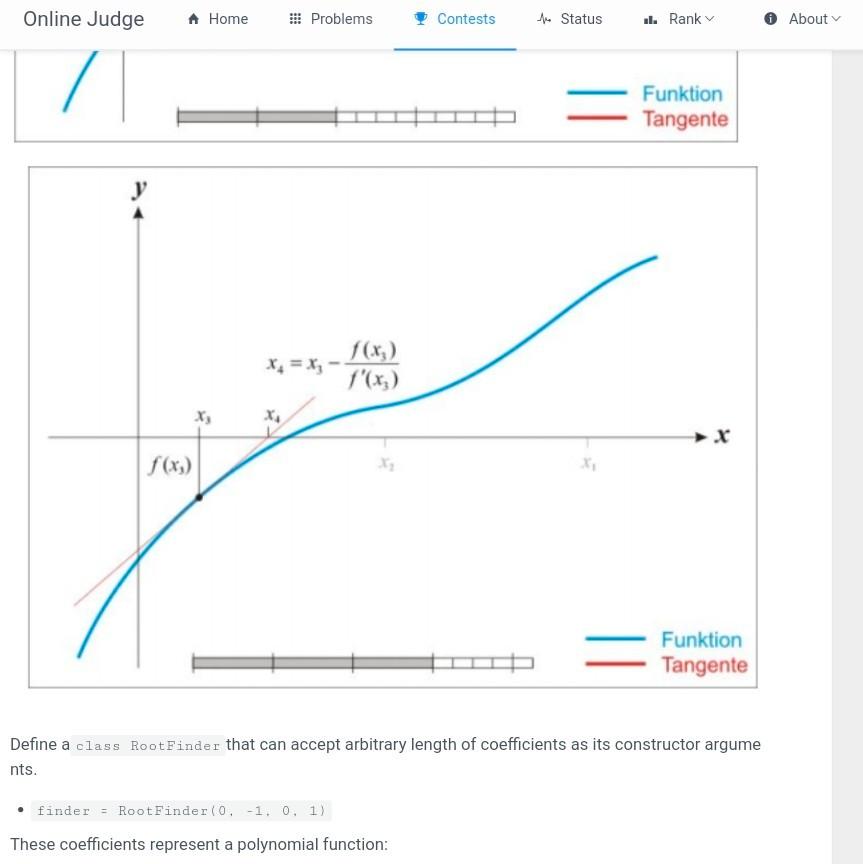
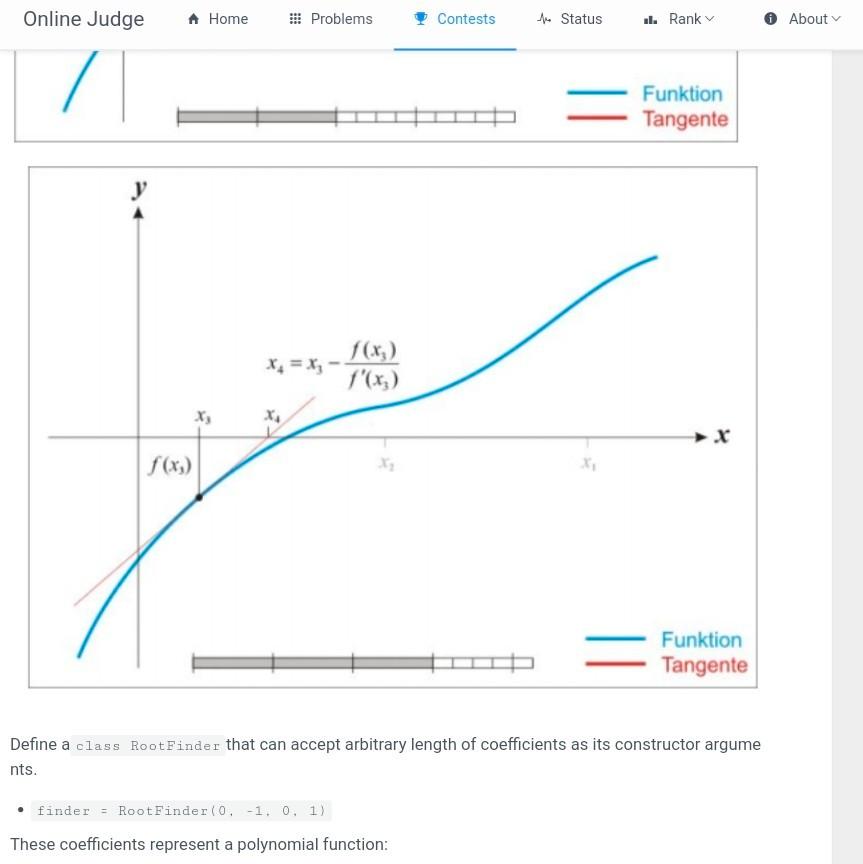
otFinder escription In numerical analysis, Newton's method is a method for finding successively better approximations to t he roots (or zeroes) of a real-valued function. It is one example of a root-finding algorithm. The method starts with a function f defined over the real numbers x, the function's derivative f, and an i nitial guess xo for a root of the function f. If the function satisfies the assumptions made in the derivati on of the formula and the initial guess is close, then a better approximation x1 is: 21 = 20 f(30) f'(x) Geometrically, (x1, 0) is the intersection of the x-axis and the tangent of the graph off at (x0, f(x0)). The process is then repeated as: 2n+1 = x f(in) f'(In) until a sufficiently accurate value is reached: |xn - Xn-11