PYTHON CODING DERIVATIVE

I will upvote whoever helps me find the derivative in python and has to pass given tests

Here's the information needed:

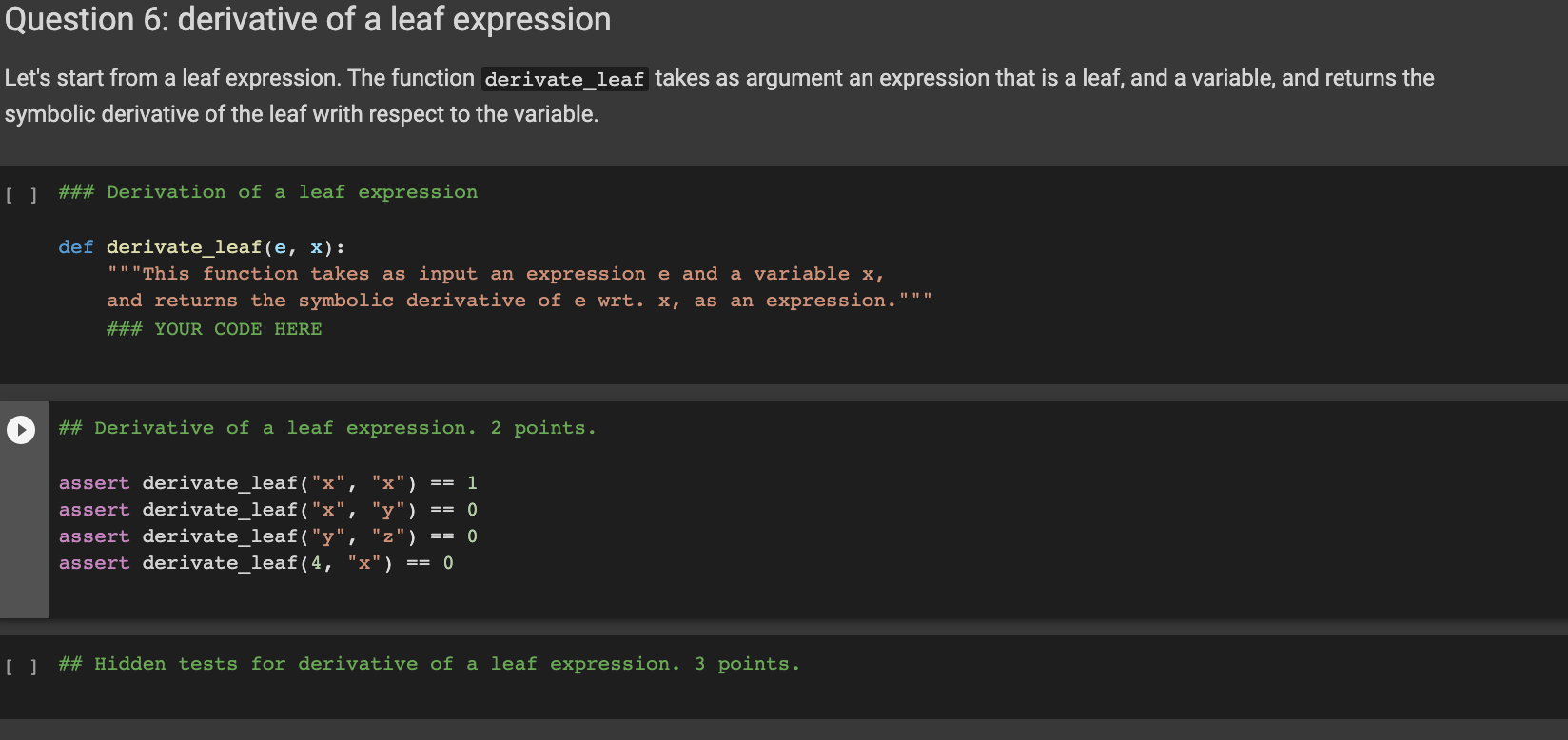
def derivate_leaf(e, x):

"""This function takes as input an expression e and a variable x,

and returns the symbolic derivative of e wrt. x, as an expression."""

### YOUR CODE HERE

## Derivative of a leaf expression. 2 points.

assert derivate_leaf("x", "x") == 1

assert derivate_leaf("x", "y") == 0

assert derivate_leaf("y", "z") == 0

assert derivate_leaf(4, "x") == 0

Derivatives Given an expression f and a variable x, we can compute symbolically the (partial) derivative of dx off with respect to x. For instance: a -(x2 + 3y + 4) = 2x d. (x+y + xy2 + 2) = 2yx + y2 +2. Here, the "partial' in partial derivative simply means: if you need to take the derivative with respect to a specific variable, simply treat all other variables as constants. Computing symbolic derivatives seems complicated, but we can take it in steps. Our expression trees have leaves, consisting of numerical constants variables and operators, corresponding to +, -, -, 7. Therefore, we break down the task into the computation of the symbolic derivative for numerical constants, variables, and arithmetic operators. The cases for the leaf nodes are: For a constant c. dc/dx = 0 . For a variable y + x, dyldx = 0. dx/dx = 1. For operators, we can use: af dg f g) = dx' af dg *g+f (9)-92 Question 6: derivative of a leaf expression Let's start from a leaf expression. The function derivate_leaf takes as argument an expression that is a leaf, and a variable, and returns the symbolic derivative of the leaf writh respect to the variable. [ ] ### Derivation of a leaf expression def derivate_leaf (e, x): """This function takes as input an expression e and a variable x, and returns the symbolic derivative of e wrt. x, as an expression.""" ### YOUR CODE HERE ## Derivative of a leaf expression. 2 points. == 1 == 0 assert derivate_leaf("x", "x") assert derivate_leaf("x", "y") assert derivate_leaf ("y", "z") assert derivate_leaf (4, "x") == == 0 0 [ ] ## Hidden tests for derivative of a leaf expression. 3 points. Derivatives Given an expression f and a variable x, we can compute symbolically the (partial) derivative of dx off with respect to x. For instance: a -(x2 + 3y + 4) = 2x d. (x+y + xy2 + 2) = 2yx + y2 +2. Here, the "partial' in partial derivative simply means: if you need to take the derivative with respect to a specific variable, simply treat all other variables as constants. Computing symbolic derivatives seems complicated, but we can take it in steps. Our expression trees have leaves, consisting of numerical constants variables and operators, corresponding to +, -, -, 7. Therefore, we break down the task into the computation of the symbolic derivative for numerical constants, variables, and arithmetic operators. The cases for the leaf nodes are: For a constant c. dc/dx = 0 . For a variable y + x, dyldx = 0. dx/dx = 1. For operators, we can use: af dg f g) = dx' af dg *g+f (9)-92 Question 6: derivative of a leaf expression Let's start from a leaf expression. The function derivate_leaf takes as argument an expression that is a leaf, and a variable, and returns the symbolic derivative of the leaf writh respect to the variable. [ ] ### Derivation of a leaf expression def derivate_leaf (e, x): """This function takes as input an expression e and a variable x, and returns the symbolic derivative of e wrt. x, as an expression.""" ### YOUR CODE HERE ## Derivative of a leaf expression. 2 points. == 1 == 0 assert derivate_leaf("x", "x") assert derivate_leaf("x", "y") assert derivate_leaf ("y", "z") assert derivate_leaf (4, "x") == == 0 0 [ ] ## Hidden tests for derivative of a leaf expression. 3 points