python

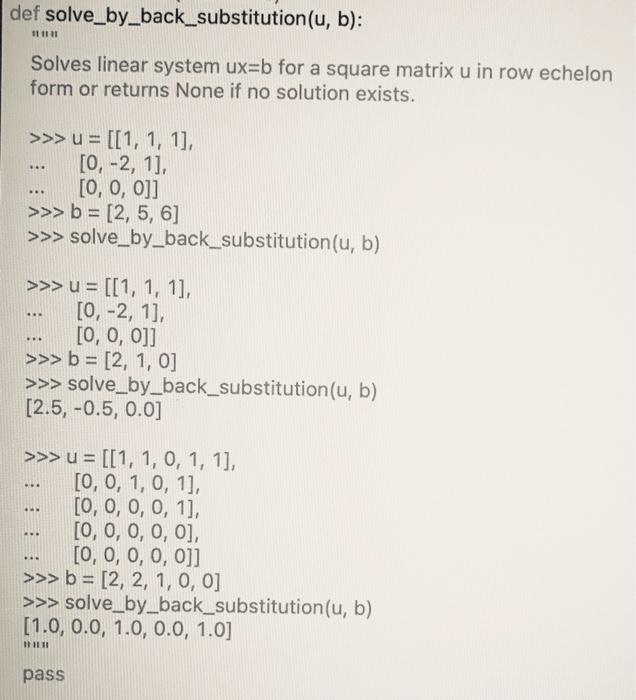
Part C: General Back Substitution If the advanced forward elimination algorithm from Part B found a pivot element in column j, it will be the edge of a stair in the staircase pattern of the output matrix (which was therefore also called "pivot' in the definition of row echelon form). All variables (columns) in the linear system can be classified as either pivot variables' (if they have a pivot/edge in their column) or "free variable if they have not. Write a modified version of the function solve by.back substution from the lecture that accepts a matrix u in row echelon form and a right-hand-side vector band returns as output: None, if the system has no solution (Hint: This can be determined simply by checking whether the right-hand-side vector has a non-zero entry in any of the all-zero rows of the matrix) A solution where all entries corresponding to free variables are 0 (Hint: All other values are then uniquely determined). For example: >>> u - ((1, 1, 1). [0, -2, 1) [0, 0, 0]] [2, 5, 6] >>> solve_by_back_substitution (u, b) >>> u - [[1, 1, 1). [0, -2, 1). [0, 0, 0]] >>> b = (2, 1, 0] >>> solve_by_back_substitution (u, b) (2.5, -0.5, 0.0] ... >>> U- [[1, 1, 0, 1, 1], [0, 0, 1, 0, 1). [0, 0, 0, 0, 1). [0, 0, 0, 0, 0], [0, 0, 0, 0, 0]] >>> b- [2, 2, 1, 0, 0] >>> solve_by_back_substitution(u, b) (1.0, 0.0, 1.0, 0.0, 1.0) def solve_by_back_substitution(u, b): 111111 Solves linear system ux=b for a square matrix u in row echelon form or returns None if no solution exists. >>> u = [[1, 1, 1], [0, -2, 1], [0, 0, 0]] >>> b = [2, 5, 6] >>> solve_by_back_substitution(u, b) . >>> u = [[1, 1, 1] [O, -2, 1], [0, 0, 0]] >>> b = [2, 1, 0] >>> solve_by_back_substitution(u, b) [2.5, -0.5, 0.0] .. . >>> u = [[1, 1, 0, 1, 1], [0, 0, 1, 0, 1], [0, 0, 0, 0, 1], [0, 0, 0, 0, 0], [0, 0, 0, 0, 0]] >>> b = [2, 2, 1, 0, 0] >>> solve_by_back_substitution(u, b) [1.0, 0.0, 1.0, 0.0, 1.0] HII II pass