Python pls. thanks

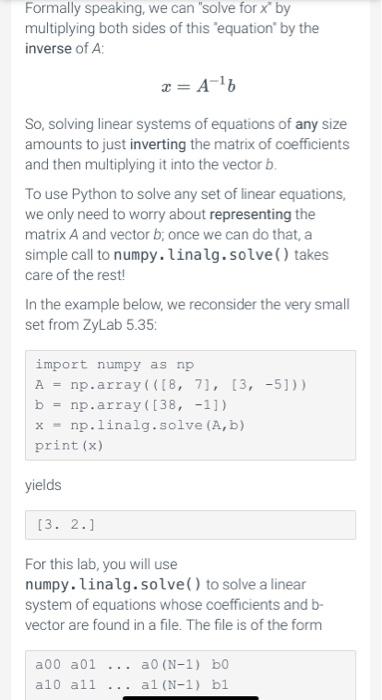
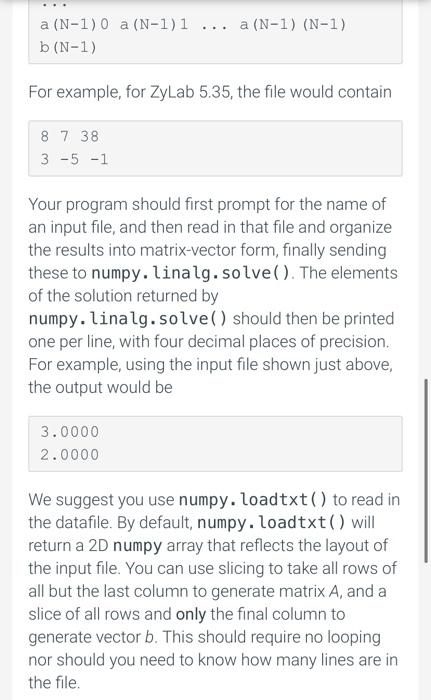
Solution of systems of multiple equations in multiple unknowns is a common engineering task. When those equations are linear, meaning the unknowns only appear to the first power and never multiplied together, the concepts of linear algebra are used to solve the system. An example of a system of linear equations appeared in ZyLab 5.35: 8x + y = 38 3x - 5y = -1 You can solve that by hand to show that x = 3 and y =-2. This linear system has only two variables, and hence four coefficients. Generally, any linear system of Nequations in N unknowns Xo, X1, X2, XN- 1, can be expressed: 200X0 + 2011] + ...20N-1&N-1 = bo 01020 +2111 +... 01,N-12N-1 = b UN-1,020 + an-1,121 +... AN-1,N-1%N-1 = where we now have a matrix of coefficients aj and a vector of b-values b;, where i andj run from 0 to N-1. Let's call the matrix A and the vector b, for simplicity. Let the ordered list of unknowns Xo, X2, X2, XN-7 be expressed just x. Then the entire set of equations can now be very compactly written Ax = b Formally speaking, we can "solve for x by multiplying both sides of this equation by the inverse of A x= A-16 So, solving linear systems of equations of any size amounts to just inverting the matrix of coefficients and then multiplying it into the vector b. To use Python to solve any set of linear equations, we only need to worry about representing the matrix A and vector b; once we can do that, a simple call to numpy. linalg.solve() takes care of the rest! In the example below, we reconsider the very small set from ZyLab 5.35: import numpy as np A = np.array( ([8, 71, [3, -5])) b = np.array([38, -1]) x = np.linalg.solve (A,b) print (x) yields [3. 2.] For this lab, you will use numpy. linalg.solve() to solve a linear system of equations whose coefficients and b- vector are found in a file. The file is of the form a00 a01 ... a0 (N-1) bo all all al (N-1) b1 a (N-1) 0 a (N-1)1 ... a (N-1) (N-1) b(N-1) For example, for ZyLab 5.35, the file would contain 8 7 38 3 -5 -1 Your program should first prompt for the name of an input file, and then read in that file and organize the results into matrix-vector form, finally sending these to numpy. linalg. solve(). The elements of the solution returned by numpy. linalg.solve() should then be printed one per line, with four decimal places of precision. For example, using the input file shown just above, the output would be 3.0000 2.0000 We suggest you use numpy.loadtxt() to read in the datafile. By default, numpy.loadtxt() will return a 2D numpy array that reflects the layout of the input file. You can use slicing to take all rows of all but the last column to generate matrix A, and a slice of all rows and only the final column to generate vector b. This should require no looping nor should you need to know how many lines are in the file