Python Programing

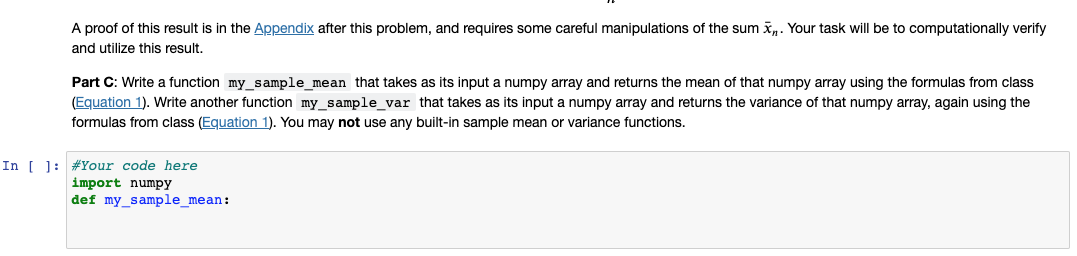
(15 pts) Problem 3: Computation (Streaming Means) Data science is often divided into two categories: questions of what the best value might be to repreesnt a data problem, and questions of how to compute that data value. Question 1 - and prior lectures - should tell you that computing the mean is valuable! But how do we compute the mean? Let X1, X2, ..., xn ben observations of a variable of interest. Recall that the sample mean n and sample variance s are given by 1 1 XX and s2 = (x2 #m] (Equation 1) n k=1 Part A: How many computations - floating point operations: addition, subtraction, multiplication, division each count as 1 operation - are required to compute the mean of the data set with n observations? Answer Typeset your result for Problem A in this cell. Part B: Now suppose our data is streaming- we slowly add observations one at a time, instead of seeing the entire data set at once. We are still interested in the mean, so if we stream the data set [4,6,0,10, ...), we first compute the mean of the the first data point [4] , then we recompute the mean of the first two points [4,6], then we recompute the mean of three [4,6,0], and so forth. Suppose we recompute the mean from scratch after each and every one of our n observations are one-by-one added to our data set. How many floating point operations are spent computing (and re-computing) the mean of the data set? Typeset your result for Problem B in this cell. We should be convinced that streaming a mean costs a lot more computer time than just computing once! In this problem we explore a smarter method for such an online computation of the mean. Result: The following relation holds between the mean of the first n - 1 observations and the mean of all n observations: xn-in-1 in = in-1 + n A proof of this result is in the Appendix after this problem, and requires some careful manipulations of the sum in. Your task will be to computationally verify and utilize this result. Part C: Write a function my_sample_mean that takes as its input a numpy array and returns the mean of that numpy array using the formulas from class (Equation 1). Write another function my_sample_var that takes as its input a numpy array and returns the variance of that numpy array, again using the formulas from class (Equation 1). You may not use any built-in sample mean or variance functions. In [ ]: #Your code here import numpy def my_sample_mean