python project in Physics

LINK

https://www.wired.com/2015/03/determining-maximum-projectile-range-numerical-model/

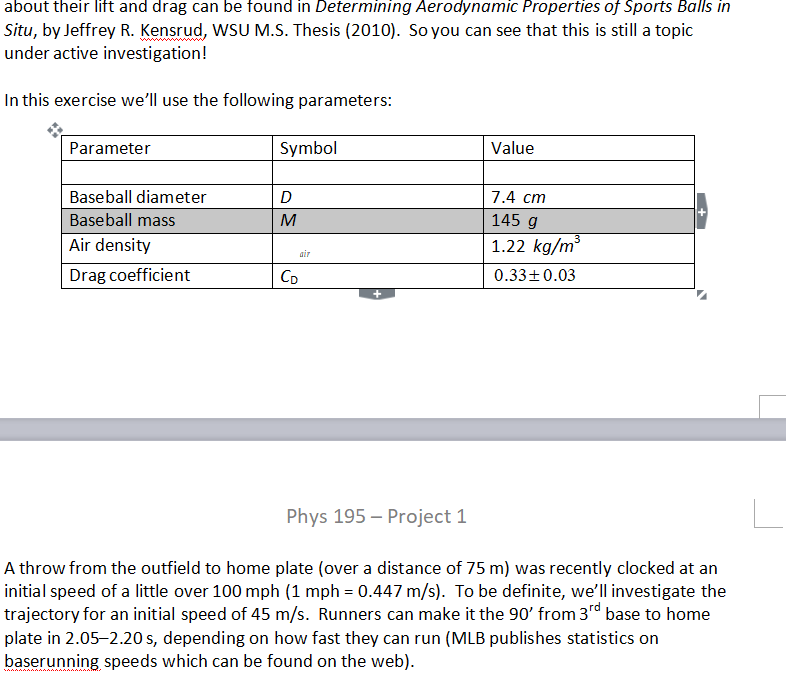
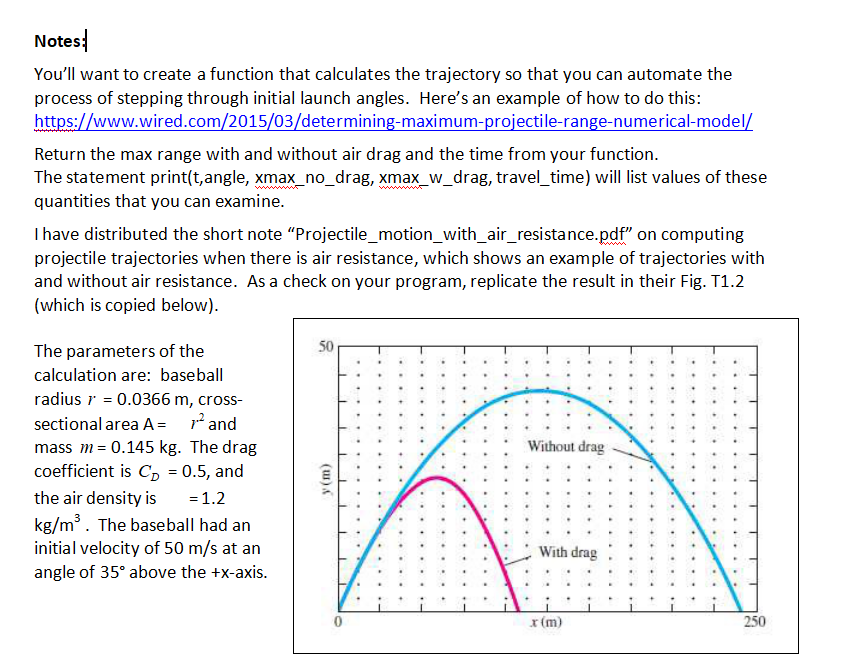
Phys 195- Project1 In Major League Baseball (MLB) there are examples of runners starting from 3rd base being thrown out at home plate by an outfielder at distances or 250 feet (76.2 m) or further. Many of the throws arrive without bouncing and leave the outfielder's hand with an initial speed of around 100 miles per hour (44.7 m/s). This exercise is to model such a throw using GlowScript with the inclusion of realistic aerodynamic drag, and to compare the travel time of the throw to the time it takes a typical runner to go the 90 feet (27.5 m) from 3rd base to home Videos of some throws can be seen at: http://m.mlb.com/cutfour/2015/11/28/157674906/10-fastest-outfield-throws-to-home-plate The added resistance of aerodynamic drag makes the trajectories of projectiles differ considerably from the ideal parabolic form we have calculated when drag is ignored. The vector force FD (i.e. "drag") on a non-streamlined body (also called a "bluff body") moving at high speed with relative vector velocity v through a fluid can be written as where denotes the volumetric density (mass/volume) of the fluid, A is the cross-sectional area of the body perpendicular to v, and C is known as the drag coefficient. We'll calculate the motion of a baseball through air, assuming that we can model the baseball as a sphere. The stitches on a baseball make the drag depend on the orientation of the ball although their effect is less for the balls used in MLB because the stitches are fairly flat. But thrown baseballs (except "knuckleball" pitches) have spin, which tends to smooth out the dependence on orientation. However, spin has a strong effect on lift, and so affects the trajectory in that way, although it has a weaker effect on drag. It is difficult to quantify these effects without knowing the rotation rate of the ball, but it appears that for modest rotation rates the drag coefficient at 100 mph is in the range 0.3-0.36. So for our model we'll ignore the lift effect and use a drag coefficient of 0.33t0.03 The properties of baseballs used in MLB are specified in section 1.09 of the MLB rulebook (http://mlb.mlb.com/mlb/downloads/y2014/official baseballrules.pdf), and more information Phys 195- Project1 In Major League Baseball (MLB) there are examples of runners starting from 3rd base being thrown out at home plate by an outfielder at distances or 250 feet (76.2 m) or further. Many of the throws arrive without bouncing and leave the outfielder's hand with an initial speed of around 100 miles per hour (44.7 m/s). This exercise is to model such a throw using GlowScript with the inclusion of realistic aerodynamic drag, and to compare the travel time of the throw to the time it takes a typical runner to go the 90 feet (27.5 m) from 3rd base to home Videos of some throws can be seen at: http://m.mlb.com/cutfour/2015/11/28/157674906/10-fastest-outfield-throws-to-home-plate The added resistance of aerodynamic drag makes the trajectories of projectiles differ considerably from the ideal parabolic form we have calculated when drag is ignored. The vector force FD (i.e. "drag") on a non-streamlined body (also called a "bluff body") moving at high speed with relative vector velocity v through a fluid can be written as where denotes the volumetric density (mass/volume) of the fluid, A is the cross-sectional area of the body perpendicular to v, and C is known as the drag coefficient. We'll calculate the motion of a baseball through air, assuming that we can model the baseball as a sphere. The stitches on a baseball make the drag depend on the orientation of the ball although their effect is less for the balls used in MLB because the stitches are fairly flat. But thrown baseballs (except "knuckleball" pitches) have spin, which tends to smooth out the dependence on orientation. However, spin has a strong effect on lift, and so affects the trajectory in that way, although it has a weaker effect on drag. It is difficult to quantify these effects without knowing the rotation rate of the ball, but it appears that for modest rotation rates the drag coefficient at 100 mph is in the range 0.3-0.36. So for our model we'll ignore the lift effect and use a drag coefficient of 0.33t0.03 The properties of baseballs used in MLB are specified in section 1.09 of the MLB rulebook (http://mlb.mlb.com/mlb/downloads/y2014/official baseballrules.pdf), and more information