PYTHONG ON JUPYTER NOTEBOOK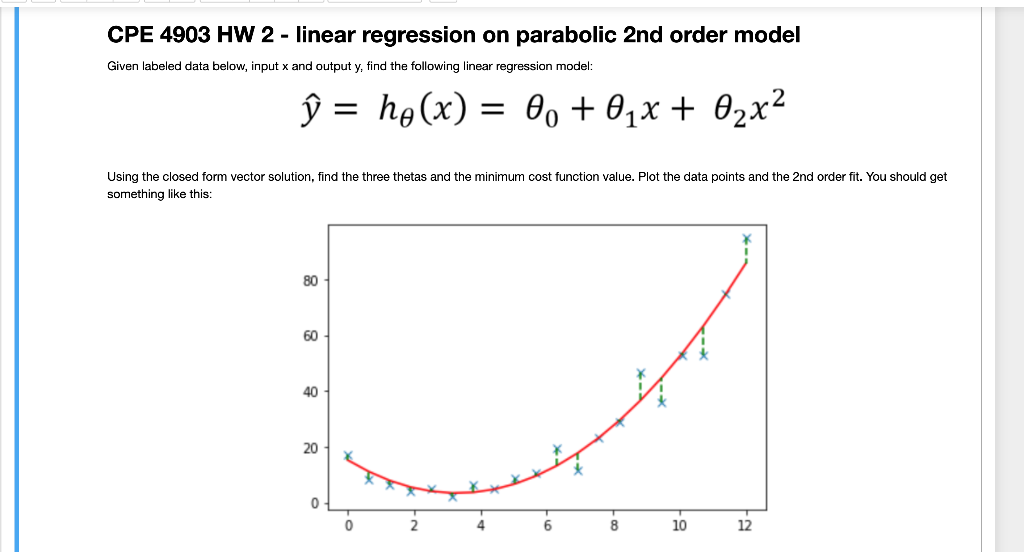

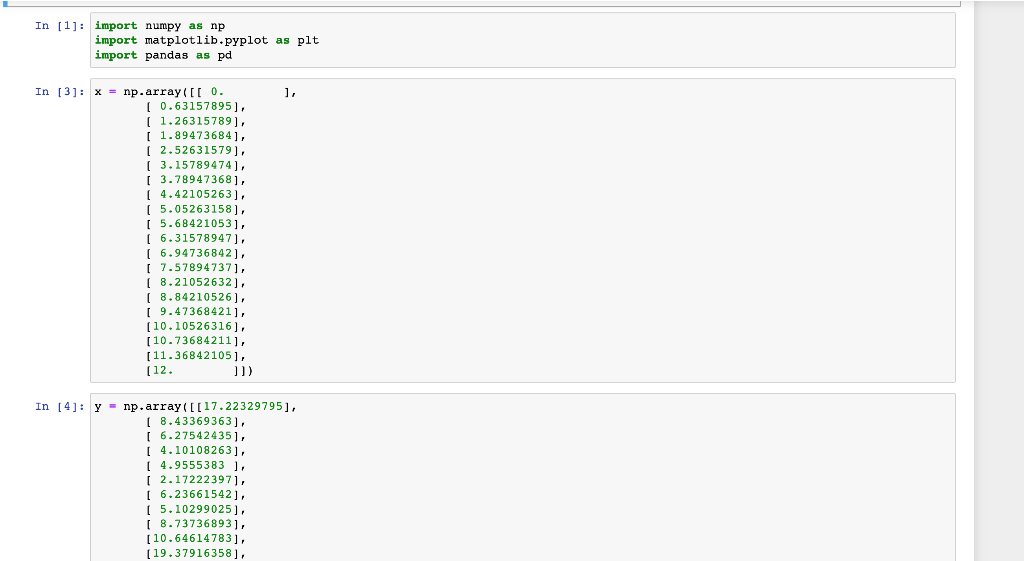
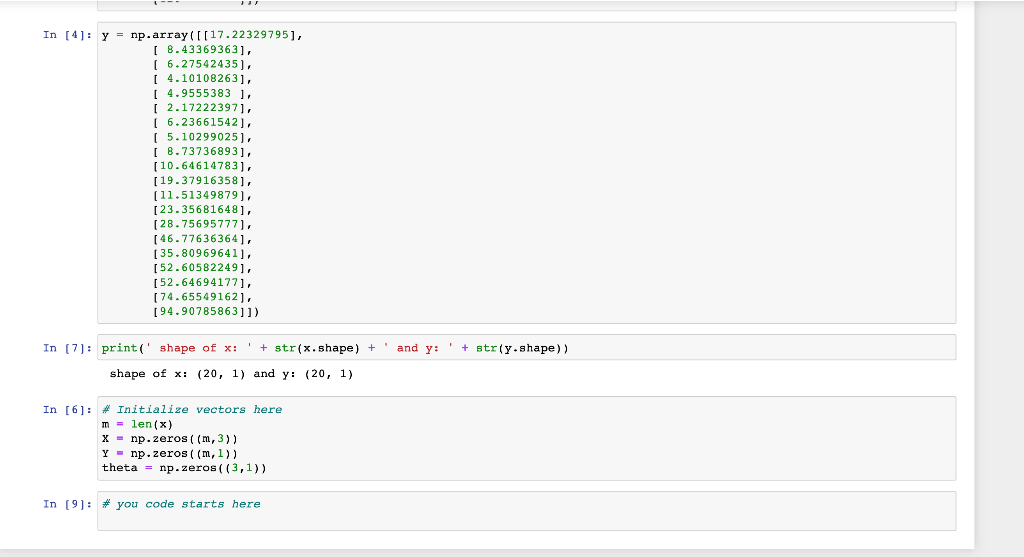
CPE 4903 HW 2 - linear regression on parabolic 2nd order model Given labeled data below, input x and output y, find the following linear regression mode y^=h(x)=0+1x+2x2 Using the closed form vector solution, find the three thetas and the minimum cost function value. Plot the data points and the 2nd order fit. You should get something like this In [3]: x=nparray([[0.[0.63157895],[1.26315789],[1.89473684],[2.52631579],[3.15789474],[3.78947368],[4.42105263],[5.05263158],[5.68421053],[6.31578947],[6.94736842],[7.57894737],[8.21052632],[8.84210526],[9.47368421],[10.10526316],[10.73684211],[11.36842105],[12. In [4]: y=nparray([[17.22329795][8.43369363][6.27542435][4.10108263][4.9555383][2.17222397][6.23661542][5.10299025][8.73736893][10.64614783][19.37916358] In [4]: y=nparray([[17.22329795],[8.43369363],[6.27542435],[4.10108263],[4.9555383],[2.17222397],[6.23661542],[8.10299025],[10.646146893],[19.37916358],[11.51349879],[23.35681648],[28.75695777],[46.77636364],[35.80969641],[52.60582249],[52.64694177],[74.65549162],[94.90785863]]) In [7]: print('shape of x:+str(x, shape )+ and y:+str(y+ shape )) shape of x:(20,1) and y:(20,1) In [6]: \# Initialize vectors here m=len(x) x=npzeros((m,3)) Y=npzeros((m,1)) theta = np.zeros ((3,1)) In [9]: \# you code starts here