Q$6.$ When $y=1,$ what is the gradient of the loss function w$.$r$.$t$.W11?$ Write your answer to three decimal places.

Note: Please use the computation graph method. One can calculate the gradient directly using chain rules, but if the computation graph is not used at all, it will not score properly. Try to fill the red boxes above. This question does not need coding and the answer can be easily obtained analytically.

Hint: You may use the property of $\frac{\text{d}\text{e}\text{l}(z)}{\text{d}\text{e}\text{l}\text{z}}=(1-)$

$0\mathrm{.}122$

Correct

Your answer is correct.

$q,$

delL

delW$11$

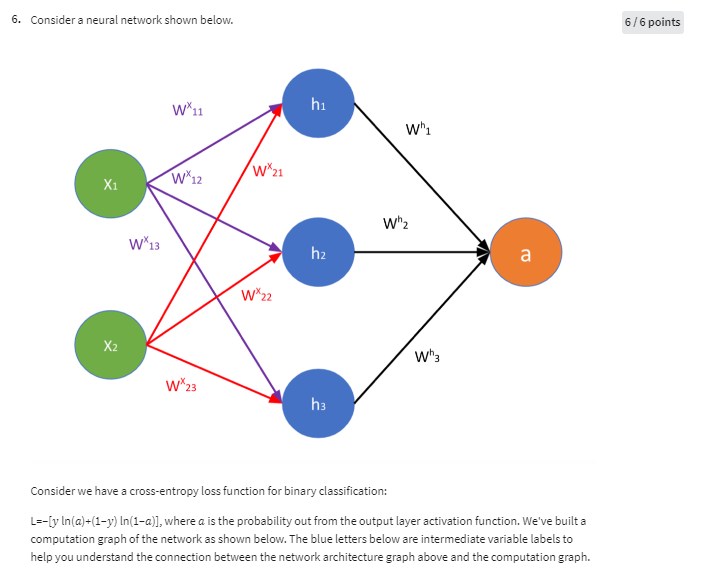
$\frac{1}{8}$ Consider a neural network shown below.

$\frac{0}{6}$ points

Consider we have a cross$-$entropy loss function for binary classification:

$L=-[yln(a)+(1-y)ln(1-a)],$ where $a$ is the probability out from the output layer activation function. We've built a computation graph of the network as shown below. The blue letters below are intermediate variable labels to help you understand the connection between the network architecture graph above and the computation graph.With the same condition $(y=1)$ and the learning rate $=\frac{1}{2},$ what is the updated weight $W21($new$)?$ Write

your answer to three decimal places.

Note: Please use the computation graph method. One can calculate the gradients directly using chain rules, but if

the computation graph is not used at all, it will not score properly. Try to fill the red boxes in the computation

graph. This question does not need coding and the answer can be easily obtained analytically.

Hint: You may use the property of $\frac{\text{d}\text{e}\text{l}(z)}{\text{d}\text{e}\text{l}\text{z}}=(1-)$

Calculate new weight using the old weight and learning learning as follows:

$W21$larrW$21-\frac{\text{d}\text{e}\text{l}\text{L}}{\text{d}\text{e}\text{l}\text{W}21}$

$1\mathrm{.}062$

Incorrect

Your answer is incorrect.

What $isW21$larrW$21-\frac{\text{d}\text{e}\text{l}\text{L}}{\text{d}\text{e}\text{l}\text{W}21}?$ Consider a neural network shown below.

$\frac{6}{6}$ points

Consider we have a cross$-$entropy loss function for binary classification:

$L=-[yln(a)+(1-y)ln(1-a)],$ where $a$ is the probability out from the output layer activation function. We've built a computation graph of the network as shown below. The blue letters below are intermediate variable labels to help you understand the connection between the network architecture graph above and the computation graph.Consider a neural network shown below. $6$ points Consider we have a cross$-$entropy loss function for binary classification: L$=-[$yln$($a$)+(1-$y$)$ln$(1-$a$)],$ where a is the probability out from the output layer activation function. We've built a computation graph of the network as shown below. The blue letters below are intermediate variable labels to help you understand the connection between the network architecture graph above and the computation graph. With the same condition $($ y$=1)$ and the learning rate $\backslash$eta $=(1)/(2),$ what is the updated weight W$21($new$)?$ Write your answer to three decimal places. Note: Please use the computation graph method. One can calculate the gradients directly using chain rules, but if the computation graph is not used at all, it will not score properly. Try to fill the red boxes in the computation graph. This question does not need coding and the answer can be easily obtained analytically. Hint: You may use the property of $($del$\backslash$sigma $($z$))/($delz$)=\backslash$sigma $(1-\backslash$sigma $)$ I need answer to be rounded to $3$ decimal points

Q$6.$ Answer is $0\mathrm{.}125$

i need answer of Q$7$