q 9 p 94 book : Computability, Complexity, and Languages by Davis, Sigal, Weyuker (Second Edition)

Book pages about the question :

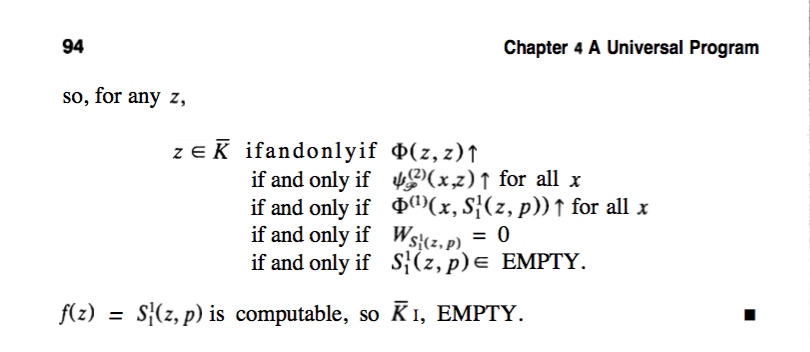
Exercises 1. Show that the proof of Theorem 4.7 is a diagonalization argument. 2. Prove by diagonalization that there is no enumeration fo fi, f2, of all total unary (not necessarily computable) functions on N. 3. Let A fx E and 4,(x)> x). (a) Show that A is re. (b) Show by diagonalization that A is not recursive. 4. Show how the diagonalization argument in the proof of Theorem 6.1 fails for the set of all numbers p such that p is the number of a program that computes a partial function, i e., the set N. 5. Let A, B be sets of numbers. Prove (a) A sm A. (b) A sm B if and only if A I, B 6. Prove that no m-complete set is recursive. 7. Let A, B be m-complete. Show that A m B. 8. Prove that R m K, ie, R is not many-one reducible to K. 9. For every number n, let A (x In EW). (a) Show that AI is r e. but not recursive, for all i. (b) Show that A m A for all i, j 10. Define the predicate P(x) 4,(x) 1. Show that POx) is not computable 11. Define the predicate Q(x) the variable Y assumes the value 1 sometime dur ing the computation of (x), where #(P) x. Exercises 1. Show that the proof of Theorem 4.7 is a diagonalization argument. 2. Prove by diagonalization that there is no enumeration fo fi, f2, of all total unary (not necessarily computable) functions on N. 3. Let A fx E and 4,(x)> x). (a) Show that A is re. (b) Show by diagonalization that A is not recursive. 4. Show how the diagonalization argument in the proof of Theorem 6.1 fails for the set of all numbers p such that p is the number of a program that computes a partial function, i e., the set N. 5. Let A, B be sets of numbers. Prove (a) A sm A. (b) A sm B if and only if A I, B 6. Prove that no m-complete set is recursive. 7. Let A, B be m-complete. Show that A m B. 8. Prove that R m K, ie, R is not many-one reducible to K. 9. For every number n, let A (x In EW). (a) Show that AI is r e. but not recursive, for all i. (b) Show that A m A for all i, j 10. Define the predicate P(x) 4,(x) 1. Show that POx) is not computable 11. Define the predicate Q(x) the variable Y assumes the value 1 sometime dur ing the computation of (x), where #(P) x