Q. Let's consider a final modification. In this version, say that whenever one firm withholds and the other floods, the firm that withholds gets 0 tomorrow and the firm that floods gets twice as much as they would otherwise receive tomorrow. This captures the idea that taking advantage of the other firm today means a greater market share tomorrow. So if both withhold, payoffs tomorrow are as in the table above. If both flood, payoffs are also as above. But if firm #1 floods and firm #2 withholds, then they receive 10 and 0 today; 12 and 0 tomorrow. Similarly, if firm #1 withholds and firm #2 floods, then they receive 2 and 6 today; 0 and 4 tomorrow. For (withhold, withhold) to be an equilibrium, p1 must be at least

and p2

must be at least

. Does the ability to capture the market make it easier or harder for firms to cooperate?

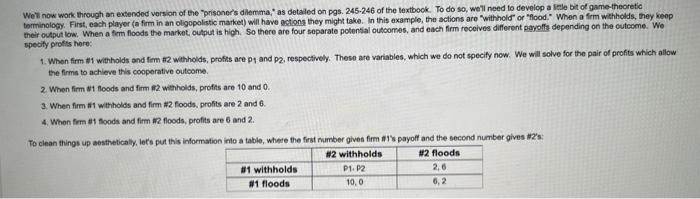
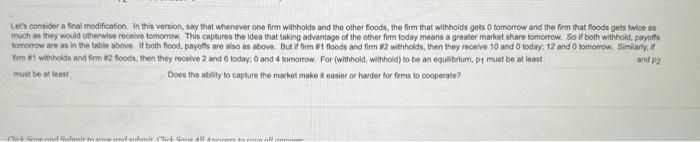
Wet now work through an excended version of the "prisoner's dilemma," as detaled on pgs. 245.246 of the textbook. To do so, weil need to develop a itile bit game-theoretic torminolocy. First, each player (a firm in an olgopolistic markel) will have actions they might takve. In this example, the actions are "with hold" or "flood." When a firm withiolds, they keep their output low. When a fiem floods the market, output is high. So there are four soparate potensial outcomes, and each firm roceives different payoffs depending on the cutcome. We specily protis hore: 1. When firm 11 withholds and fem 82 wathholds, profhs are p1 and p2, respectively. These are variables, which we do not specily now. We will solve for the pair of profits which allow the firms to achieve this cooperative outcome. 2. When firm 11 floods and firm m2 wehholds, profts are 10 and 0 . 3. When firm thi withholds and firm 42 foods, profits are 2 and 6 . 4. Whon fom th soods and firm m2 floods, profits are 6 and 2 . To ciean things up aestheticaly, lers put this information into a table, where the first mumber gives firm in1s payoff and the second number gives th2's: Leth contider a fral modification. In this vervion, say that whenever one firm withholds and the other foods, the firm that with oids gets 0 tomonow and the firm that foods gets twice as mych as they would otherwise receive lomorrow. This captures the iden that taking advantage of the other fim today means a greater markot share tomorrow. So if both witthold, payoffa must be at inast Does the abeily to capture the maket make it easier or harder for fims to cooperate? Wet now work through an excended version of the "prisoner's dilemma," as detaled on pgs. 245.246 of the textbook. To do so, weil need to develop a itile bit game-theoretic torminolocy. First, each player (a firm in an olgopolistic markel) will have actions they might takve. In this example, the actions are "with hold" or "flood." When a firm withiolds, they keep their output low. When a fiem floods the market, output is high. So there are four soparate potensial outcomes, and each firm roceives different payoffs depending on the cutcome. We specily protis hore: 1. When firm 11 withholds and fem 82 wathholds, profhs are p1 and p2, respectively. These are variables, which we do not specily now. We will solve for the pair of profits which allow the firms to achieve this cooperative outcome. 2. When firm 11 floods and firm m2 wehholds, profts are 10 and 0 . 3. When firm thi withholds and firm 42 foods, profits are 2 and 6 . 4. Whon fom th soods and firm m2 floods, profits are 6 and 2 . To ciean things up aestheticaly, lers put this information into a table, where the first mumber gives firm in1s payoff and the second number gives th2's: Leth contider a fral modification. In this vervion, say that whenever one firm withholds and the other foods, the firm that with oids gets 0 tomonow and the firm that foods gets twice as mych as they would otherwise receive lomorrow. This captures the iden that taking advantage of the other fim today means a greater markot share tomorrow. So if both witthold, payoffa must be at inast Does the abeily to capture the maket make it easier or harder for fims to cooperate