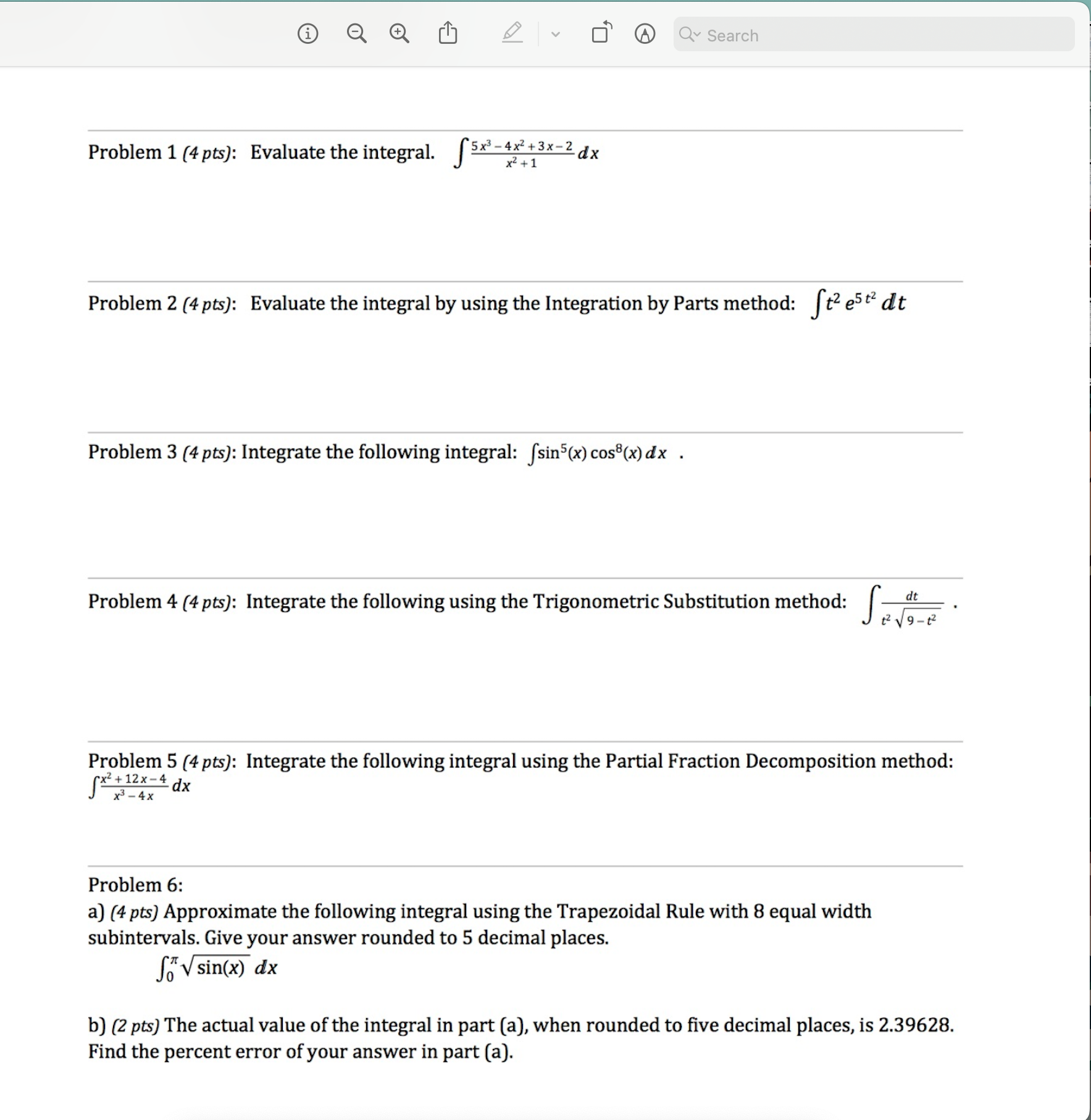
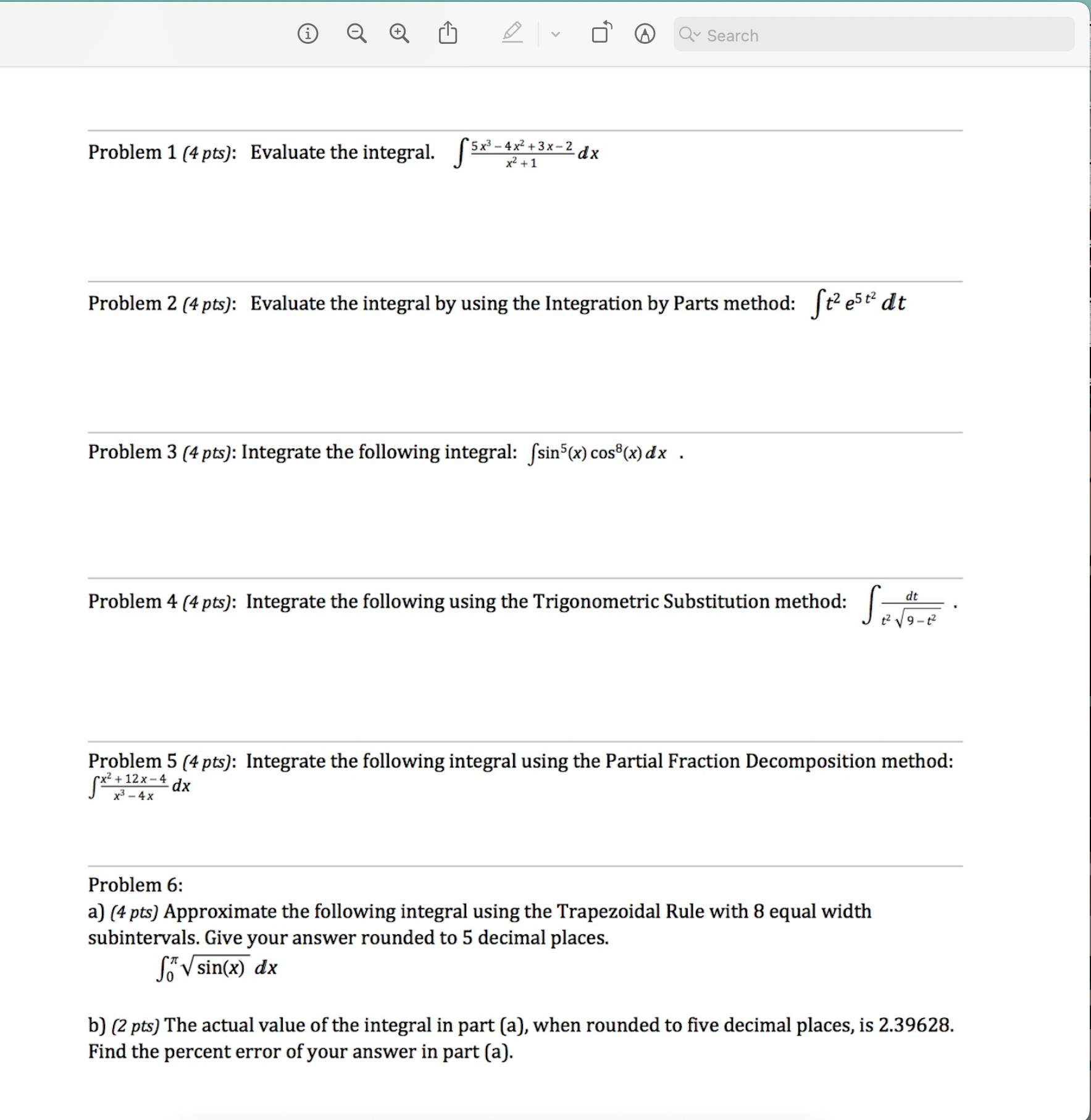
Q Search Problem 1 (4 pts): Evaluate the integral. 5x -4x +3x-2 dx x2 +1 Problem 2 (4 pts): Evaluate the integral by using the Integration by Parts method: St2 estz dt Problem 3 (4 pts): Integrate the following integral: fsin5(x) cos8(x) dx . Problem 4 (4 pts): Integrate the following using the Trigonometric Substitution method: Problem 5 (4 pts): Integrate the following integral using the Partial Fraction Decomposition method: "x2 + 12x -4 dx x3 -4x Problem 6: a) (4 pts) Approximate the following integral using the Trapezoidal Rule with 8 equal width subintervals. Give your answer rounded to 5 decimal places. o'sin(x) dx b) (2 pts) The actual value of the integral in part (a), when rounded to five decimal places, is 2.39628. Find the percent error of your answer in part (a).1 Problem 7 {4 p13): You are asked to approximate the integral L1 cos(x2) dx to an error of less than 10-5. You decide to use the Trapezoidal Rule, but you are not sure how many subintervals to use to guarantee that your error meets the requirements. So you do a quick search and nd the following theorem: THEOREM Errors in Numerical Integration Assume f " is continuous on the interval [a, b] and k is a real number such that [f" (x)| s k, for all x in [(1, b]. The absolute errors in approximating the integral fabx) dx by the Midpoint Rule and Trapezoid Rule with n subintervals satisfy the inequalities EM 5 Egg\"1m? and ET 5 Egg"1mm respectively, where Ax = bf\". a) Find an appropriate value of k such that If " (x)| s k. b] Using the above theorem, nd the smallest number of subintervals that would guarantee the error bound of 10-5. Problem 8 (4 pm): Evaluate the following integral or show why it diverges: I: X dx (x2 + 1)2 _ . . . . . . _1n3t2 _ Problem9 (4 pm). Solve the followmg 1n1t1al value problem. y (t) my , y(1)_0