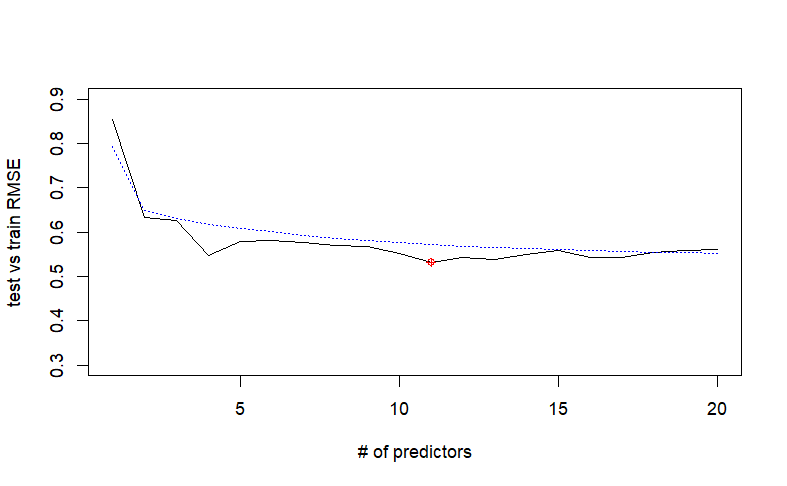
Q$.$The previous codes fit a model using the entire golf data set. The next set of code splits the data set in a training and validation set $(50/50)$ and provides the MSE metric for both sets. What does the test MSE suggest that the appropriate number of predictors should be$?$ Are there any signs of overfitting based on the graphic? What happens if you change the split to $80/20?$ explain the graph which is in image and please read the question very carefully

$```\{$r$\}$

library$($caret$)$

set.seed$(1234)$

trainIndexcreateDataPartition$($golf$2$$AvgWinnings,p$=\mathrm{.}8,$list$=$F$)$ #p: proportion of data in train

traininggolf$2[$trainIndex$,]$

validategolf$2[-$trainIndex,$]$

fwd$.$train$=$regsubsets$($log$($AvgWinnings$)$~$.,$data$=$training,method$=$"forward",nvmax$=20)$

#Creating a prediction function

predict.regsubsets $=$function $($object $,$ newdata $,$id $,...)\{$

form$=$as$.$formula $($object$call $[[2]])$

mat$=$model.matrix$($form $,$newdata $)$

coefi$=$coef$($object $,$id$=$id$)$

xvars$=$names$($coefi$)$

mat$[,$xvars$]\%*\%$coefi

$\}$

valMSEc$()$

#note my index, i$,$ is to $20$ since that is how many predictors I went up to during fwd selection

for $($i in $1$:$20)\{$

predictionspredict.regsubsets$($object$=$fwd$.$train,newdata$=$validate,id$=$i$)$

valMSE$[$imean$(($log$($validate$AvgWinnings$)-$predictions$)^2)$

$\}$

par$($mfrow$=$c$(1,1))$

plot$(1$:$20,$sqrt$($valMSE$),$type$="$l$",$xlab$="$# of predictors",ylab$=$"test vs train RMSE",ylim$=$c$(0\mathrm{.}3,\mathrm{.}9))$

indexwhich$($valMSE$==$min$($valMSE$))$

points$($index$,$sqrt$($valMSE$[$index$]),$col$=$"red",pch$=10)$

trainMSEsummary$($fwd$.$train$)$$rss$/$nrow$($training$)$

lines$(1$:$20,$sqrt$($trainMSE$),$lty$=3,$col$=$"blue"$)$