Q1:

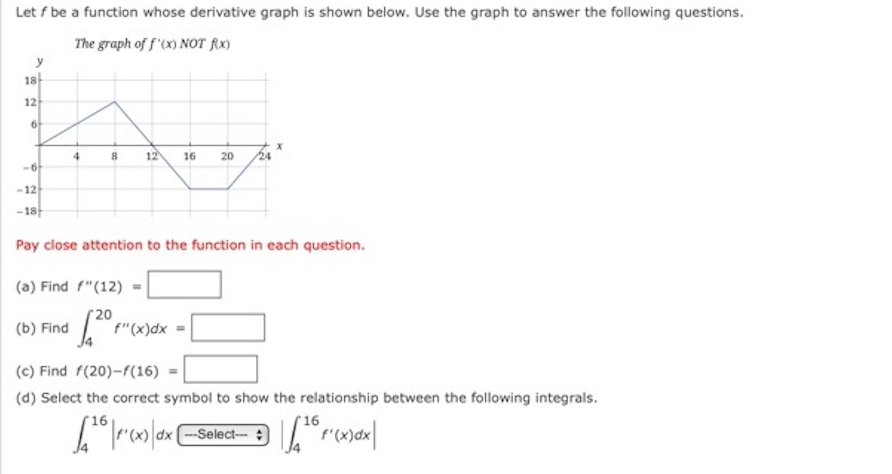
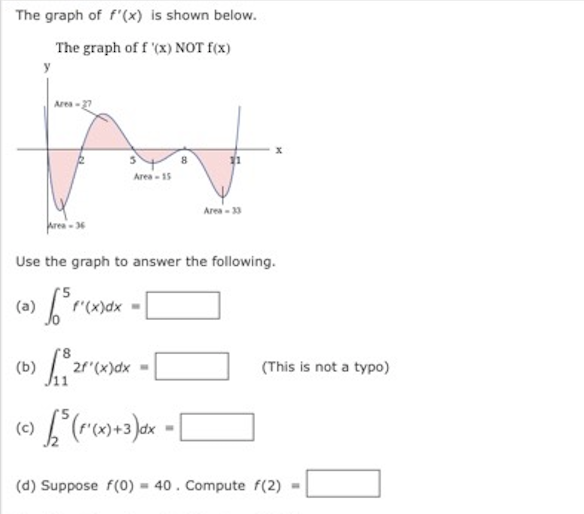
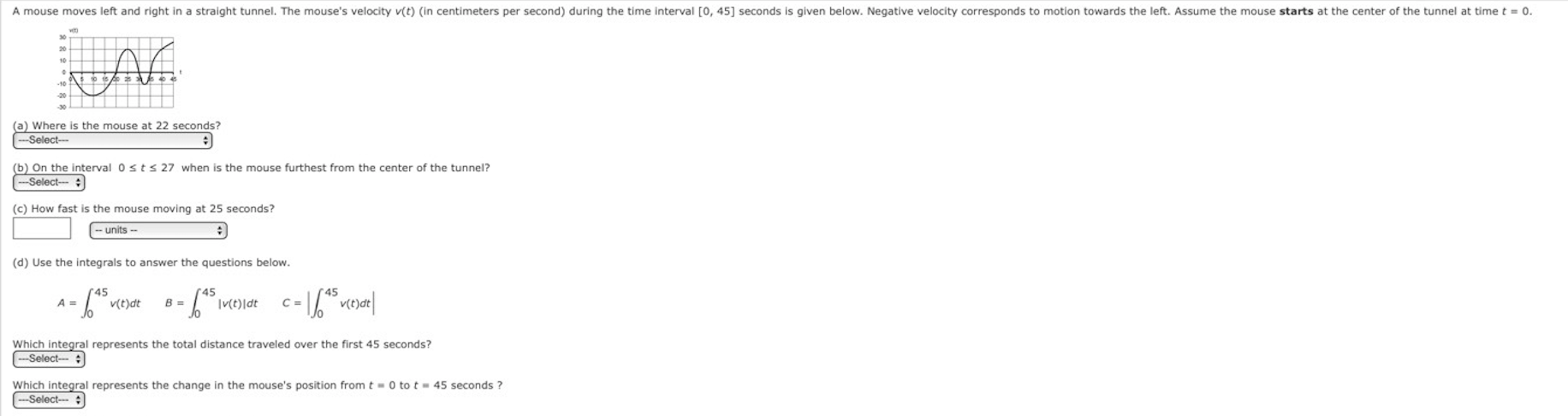
Let f be a function whose derivative graph is shown below. Use the graph to answer the following questions. The graph of f'(x) NOT Rx) y 18 12 12 16 20 -12 -18 Pay close attention to the function in each question. (a) Find f"(12) = (b) Find (c) Find f(20)-f(16) = (d) Select the correct symbol to show the relationship between the following integrals. (x) dx 16 --Select- :The graph of f'(x) is shown below. The graph of f '(x) NOT f(x) Area = 15 Area - 13 Area - 30 Use the graph to answer the following. (a) "' (x )dx (b ) 21 " ( x ) dx (This is not a typo) () 62 ( 1( x ) +3 ) Ox - (d) Suppose f(0) = 40 . Compute f(2) =Suppose g(x) is a family of continuous functions with the following derivatives. Assume M is a non-zero parameter. M g '(x) = 5Me (Mx+2) 2 M g"(x) = 20M e (Mx+2) 3 Find M so that the function g has an inflection point at x = 9 M = 10A mouse moves left and right in a straight tunnel. The mouse's velocity v(t) (in centimeters per second) during the time interval [0, 45] seconds is given below. Negative velocity corresponds to motion towards the left. Assume the mouse starts at the center of the tunnel at time t = 0. (a) Where is the mouse at 22 seconds? -Select- (b) On the interval 0 s t S 27 when is the mouse furthest from the center of the tunnel? -Select-" (c) How fast is the mouse moving at 25 seconds? - units - (d) Use the integrals to answer the questions below. A = (45 v(that B = Iveldt c = / vest | Which integral represents the total distance traveled over the first 45 seconds? -Select- : Which integral represents the change in the mouse's position from t = 0 to t = 45 seconds ? -Select- *