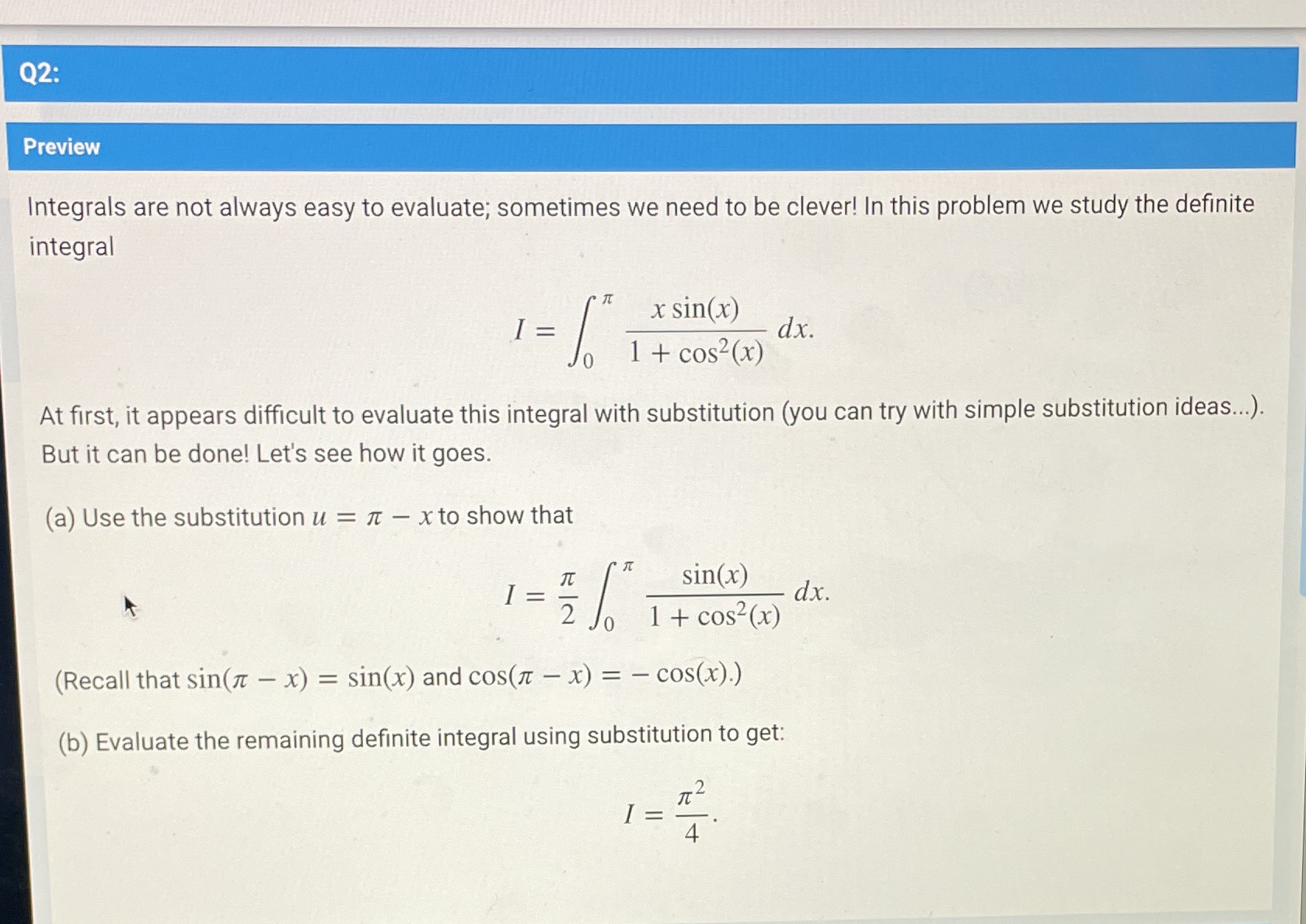
Q2: Preview Integrals are not always easy to evaluate; sometimes we need to be clever! In this problem we study the definite integral x sin(x) 1 = dx. 1 + cos2 (x) At first, it appears difficult to evaluate this integral with substitution (you can try with simple substitution ideas...). But it can be done! Let's see how it goes. (a) Use the substitution u = 7 - x to show that sin(x) 1 = 2 dx. 1 + cos2 (x) (Recall that sin(7 - x) = sin(x) and cos(n - x) = - cos(x).) (b) Evaluate the remaining definite integral using substitution to get: I = 4