Q3 . Math Real Analysis. Solve question 3 please

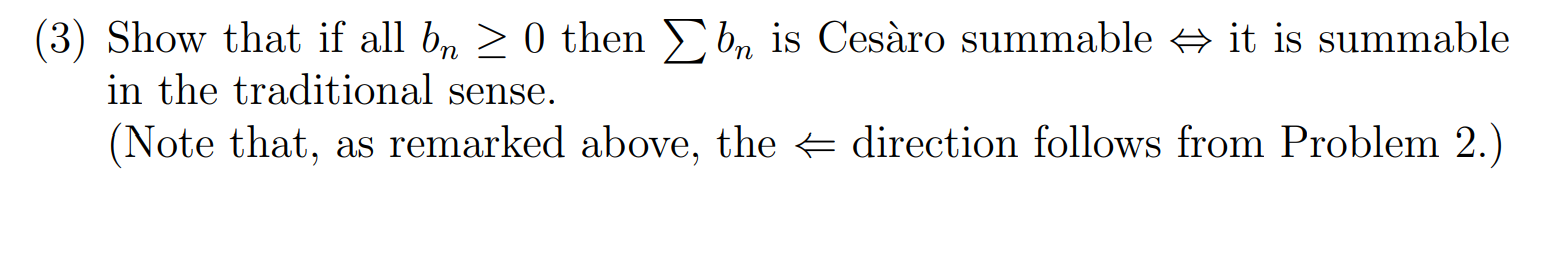
(2) Show that if a sequence an > a then it is Cesaro convergent to a as well. (Note that problem 2.2 of the text states the series version of this state ment. ie that if 2 bn is summable to b in the traditional sense, then it is also Cesaro summable to b. This follows from our problem, by applying it to the sequence of partial sums.) (3) Show that if all bn 2 0 then Ebn is Cesaro summable -> it is summable in the traditional sense. (Note that, as remarked above, the