Question: Q.4) A queue is observed over 1000 time intervals where the size of the queue after each time stop is given. Construct a simple model

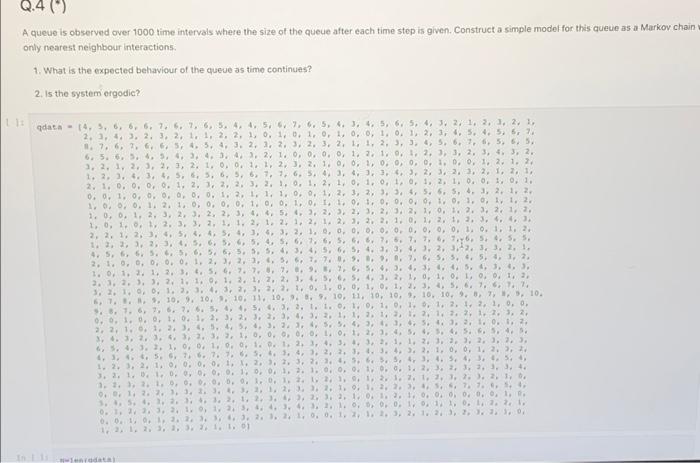
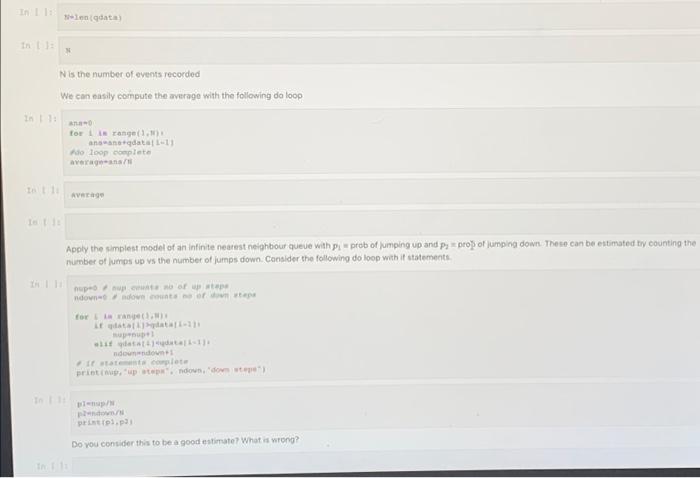
Q.4) A queue is observed over 1000 time intervals where the size of the queue after each time stop is given. Construct a simple model for this quelle as a Markov chain only nearest neighbour interactions. 1. What is the expected behaviour of the queue as timo continues? 2. Is the system ergodic? 'OTECTICUT data - 14, 5, 6, 5, 6, 7, 6, 7, 6, 5. 4. 4, 5, 6, 7, 6, 5, 4, 3, 4, 5, 6, 5, 4, 3, 2, 1, 2, 3, 2, 1) 2. 3. 4. ). 2. 3, 2, 1, 1, 2, 2, 1, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0.1, 2, 3, 4, 5, 4, 5, 6, 1.7, 6, 7, 6, 54. 5. 4. 3. 2. 1. 2. 3. 2.3.2.1.1, 2, 3, 3, 4, 5, 6, 7, 6, 5, 6, 5, 6. 5. 6.5, 5, 4, 3. 4.3. 4.3. 2 1.0, 0.0.0, 1. 2. 10. 1. 2.), 3, 2, 3, 4, 3, 2. 3.2.1, 2, 3, 2, 3, 2, 1, 0, 0.1.1, 2). 2. 1.0, 0.1, 0.0 0.0.1.0.0.1, 2.1.2 1, 2, 3, 4, 3, 4, 5, 6, 5, 6, 5, 6, 7, 165, 4, 3, 4, 5, 3, 4, 5, 2, 3, 2, 3, 2, 1, 2, 1, 2. 1.0.0.0.0.1.2.1.2.2.) 2.1. 0. 1. 2. 10. 1.0.1.0, 1.2, 1.0.0.0, 1. 0.0 1.0.0.0.0.0.0. 1. 2. 1. 1. 1.0.0. 1. 2. 3. 2.). 3. 4. 5. 6. 5.4., 2. 1. 2. 1.0.0, 0. 1. 2. 1.0, 0, 0, 0.1, 0, 0, 1, 0, 1, 1.0, 1.0.0.0.0.0.1.0.1 1.2 1. 0. 01. 2. 3. 2.), 2, 2, 3, 4, 5, 4.). 2. ), 2.), 2, 3, 2, 1.0, 1. 2. 3. 2. 1. 2. 1.0, 1.0, 1, 2, 3, 3, 2, 1, 1, 2, 1.2: 1. 2. 1. 2. 3. 2. 2.1, 0. 1. 2. 1. 2. 3. 4. 4.). 2. 2. 1. 2. 3. 4. 5. 6. 4. 5. 4.) 3.2.1.0.0.0.0.0.0.0.0.0.0.1.0.1.1.2 1.2.2.2.2.3.4.5.6.5.6 5. 4. 5. 6. 7. 6. 5. 5. 6. 7. 15. 7. 7. 6. 7.6.5, 4.5, 5, 4, 5, 6, 65, 6, 5, 6, 5.5, 5, , 5, 4, 3, 4, 5, 6, 5, 4.1, 3, 4, 3, 2, 3.2.3, 3, 2, 1. 2, 1.0, 0, 0, 0, 0, 1, 2,22,2.5, 57.7.0....0. 7. 6. 5. 3. 4. 5. 41, 2 1. 01. 2. 1. 2. 3. . 5. 6. 7.7.8. 7. 8. 9... 6, 5.1.3.4.3.5.) ..). 2.1.2.). ), 2:1 1.9. 1. 2. 1. 2. 2. 4. 5. 6. 5. 4.). 2, 1.0, 1.0.1.0.0.1.3 3.2.1, 0, 0, 1, 2, 3, 4, 3, 2, 3, 2, , 1.0, 1.0, 0, 1, 0, 1, 23, 4, 5, 6, 7, 6, 7. 7 1.3.1. 10. 10. 10. 11. 10. ... 10, 11, 10, 10, 10, 10.9, 8, 7, 10, $.3. 1. 6, , S. 26. 5.4.4.5.3.2.1.1.0.0, 1.0, 1.0, 1.2, 1.2.1.0.0. 0.0.1.0.0.1. 01. 2. 3. 2. 3. 2. 3. 4.3.2.1.1.2.1.2.1.2.1.1.2.1.2.). 2 2.2.1. 01. 2. 3. 4. 5.4 5.3.2.2., 3........... 3.1. 0.1.2 2.3.2.3.4.2.3.3.1.0.0.0.0.0.1. 01. 2. 3. 4. 5. 6. 4. 5. 6. 5. 4.) 3. 4.3.), 1.0, 0. 1.0.0.1.0.1, 2, 3, 4, 3, , 3, 2, 1. 1. 2. 3. 3.), 2.), ). 4.) 4. 5. 6. 76. 7.7.8.9.6.1.4), 2, 2.3.3.4. ). 2. 1.0.0.1.2. >, 1.2. ), 2. 1.0.0.0.0.1.1.2.), 7. 3. 2. 3. 4. 5. 6.3.5, 4, 3, 4, 3, 4, 5, 3.2.1., 1.0, 0, 0, 0, 0, 0, 0, 1). O, 0, 0.1, 0. 1. 2. 3. 2. 3. 3.3.3.4 1.1.1.1.,0,0,0,0,1,0,1,1,1,2,1,3,1,3,3,.) ... 0.3 1.2.2.). 1. 2. 3. 4.3.2.1.2.3.2.1, 1.2, 2., 5, 6, 7, 1... 3.5. . . . . . . . 12)..), ).3.1.0.1.1.0.0, 0, 0, 0, 0, 1, 0.1.2.3, 1.0, 1.33...), ), 1.0, 0, 0, 1.0, 1.0.1.3.2.1. 0.0.1.1.2.2.3.4.3.2.1.1.0.0, 12, 13, 2, 1 ..... 11. 2. 3.1, 3.1.01 " " SS SS OOOTEEEEEE en data Nis the number of events recorded We can easily compute the average with the following de loop for range(11) anandata13 Ado loop complete average AVAT Apply the simplest model of an infinite nearest neighbour queue with pi prob of jumping up and Pros of jumping down. These can be estimated try counting the number of Jump up vs the number of jumps down. Consider the following do loop with it statements pop ndowne down on tape for many Ltda data ndonos state complete pritiup down, dost /N pando prip: Do you consider this to be a good estimate? What is wrong? Q.4) A queue is observed over 1000 time intervals where the size of the queue after each time stop is given. Construct a simple model for this quelle as a Markov chain only nearest neighbour interactions. 1. What is the expected behaviour of the queue as timo continues? 2. Is the system ergodic? 'OTECTICUT data - 14, 5, 6, 5, 6, 7, 6, 7, 6, 5. 4. 4, 5, 6, 7, 6, 5, 4, 3, 4, 5, 6, 5, 4, 3, 2, 1, 2, 3, 2, 1) 2. 3. 4. ). 2. 3, 2, 1, 1, 2, 2, 1, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0.1, 2, 3, 4, 5, 4, 5, 6, 1.7, 6, 7, 6, 54. 5. 4. 3. 2. 1. 2. 3. 2.3.2.1.1, 2, 3, 3, 4, 5, 6, 7, 6, 5, 6, 5, 6. 5. 6.5, 5, 4, 3. 4.3. 4.3. 2 1.0, 0.0.0, 1. 2. 10. 1. 2.), 3, 2, 3, 4, 3, 2. 3.2.1, 2, 3, 2, 3, 2, 1, 0, 0.1.1, 2). 2. 1.0, 0.1, 0.0 0.0.1.0.0.1, 2.1.2 1, 2, 3, 4, 3, 4, 5, 6, 5, 6, 5, 6, 7, 165, 4, 3, 4, 5, 3, 4, 5, 2, 3, 2, 3, 2, 1, 2, 1, 2. 1.0.0.0.0.1.2.1.2.2.) 2.1. 0. 1. 2. 10. 1.0.1.0, 1.2, 1.0.0.0, 1. 0.0 1.0.0.0.0.0.0. 1. 2. 1. 1. 1.0.0. 1. 2. 3. 2.). 3. 4. 5. 6. 5.4., 2. 1. 2. 1.0.0, 0. 1. 2. 1.0, 0, 0, 0.1, 0, 0, 1, 0, 1, 1.0, 1.0.0.0.0.0.1.0.1 1.2 1. 0. 01. 2. 3. 2.), 2, 2, 3, 4, 5, 4.). 2. ), 2.), 2, 3, 2, 1.0, 1. 2. 3. 2. 1. 2. 1.0, 1.0, 1, 2, 3, 3, 2, 1, 1, 2, 1.2: 1. 2. 1. 2. 3. 2. 2.1, 0. 1. 2. 1. 2. 3. 4. 4.). 2. 2. 1. 2. 3. 4. 5. 6. 4. 5. 4.) 3.2.1.0.0.0.0.0.0.0.0.0.0.1.0.1.1.2 1.2.2.2.2.3.4.5.6.5.6 5. 4. 5. 6. 7. 6. 5. 5. 6. 7. 15. 7. 7. 6. 7.6.5, 4.5, 5, 4, 5, 6, 65, 6, 5, 6, 5.5, 5, , 5, 4, 3, 4, 5, 6, 5, 4.1, 3, 4, 3, 2, 3.2.3, 3, 2, 1. 2, 1.0, 0, 0, 0, 0, 1, 2,22,2.5, 57.7.0....0. 7. 6. 5. 3. 4. 5. 41, 2 1. 01. 2. 1. 2. 3. . 5. 6. 7.7.8. 7. 8. 9... 6, 5.1.3.4.3.5.) ..). 2.1.2.). ), 2:1 1.9. 1. 2. 1. 2. 2. 4. 5. 6. 5. 4.). 2, 1.0, 1.0.1.0.0.1.3 3.2.1, 0, 0, 1, 2, 3, 4, 3, 2, 3, 2, , 1.0, 1.0, 0, 1, 0, 1, 23, 4, 5, 6, 7, 6, 7. 7 1.3.1. 10. 10. 10. 11. 10. ... 10, 11, 10, 10, 10, 10.9, 8, 7, 10, $.3. 1. 6, , S. 26. 5.4.4.5.3.2.1.1.0.0, 1.0, 1.0, 1.2, 1.2.1.0.0. 0.0.1.0.0.1. 01. 2. 3. 2. 3. 2. 3. 4.3.2.1.1.2.1.2.1.2.1.1.2.1.2.). 2 2.2.1. 01. 2. 3. 4. 5.4 5.3.2.2., 3........... 3.1. 0.1.2 2.3.2.3.4.2.3.3.1.0.0.0.0.0.1. 01. 2. 3. 4. 5. 6. 4. 5. 6. 5. 4.) 3. 4.3.), 1.0, 0. 1.0.0.1.0.1, 2, 3, 4, 3, , 3, 2, 1. 1. 2. 3. 3.), 2.), ). 4.) 4. 5. 6. 76. 7.7.8.9.6.1.4), 2, 2.3.3.4. ). 2. 1.0.0.1.2. >, 1.2. ), 2. 1.0.0.0.0.1.1.2.), 7. 3. 2. 3. 4. 5. 6.3.5, 4, 3, 4, 3, 4, 5, 3.2.1., 1.0, 0, 0, 0, 0, 0, 0, 1). O, 0, 0.1, 0. 1. 2. 3. 2. 3. 3.3.3.4 1.1.1.1.,0,0,0,0,1,0,1,1,1,2,1,3,1,3,3,.) ... 0.3 1.2.2.). 1. 2. 3. 4.3.2.1.2.3.2.1, 1.2, 2., 5, 6, 7, 1... 3.5. . . . . . . . 12)..), ).3.1.0.1.1.0.0, 0, 0, 0, 0, 1, 0.1.2.3, 1.0, 1.33...), ), 1.0, 0, 0, 1.0, 1.0.1.3.2.1. 0.0.1.1.2.2.3.4.3.2.1.1.0.0, 12, 13, 2, 1 ..... 11. 2. 3.1, 3.1.01 " " SS SS OOOTEEEEEE en data Nis the number of events recorded We can easily compute the average with the following de loop for range(11) anandata13 Ado loop complete average AVAT Apply the simplest model of an infinite nearest neighbour queue with pi prob of jumping up and Pros of jumping down. These can be estimated try counting the number of Jump up vs the number of jumps down. Consider the following do loop with it statements pop ndowne down on tape for many Ltda data ndonos state complete pritiup down, dost /N pando prip: Do you consider this to be a good estimate? What is wrong

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

qdata = [4, 5, 6, 6, 6, 7, 6, 7, 6, 5, 4, 4, 5, 6, 7, 6, 5, 4, 3, 4, 5, 6, 5, 4, 3, 2, 1, 2, 3, 2, 1, 2, 3, 4, 3, 2, 3, 2, 1, 1, 2, 2, 1, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 1, 2, 3, 4, 5, 4, 5, 6, 7, 8,...

maple 4. (*) A queue is observed over 1000 time intervals where the size of the queue after each time step is given. Construct a simple model for this queue as a Markov chain with only nearest...

A queue is observed over 1000 time intervals where the size of the queue after each time step is given. Construct a simple model for this queue as a Markov chain with only nearest neighbour...

qdata = [5, 5, 5, 6, 5, 6, 6, 7, 6, 5, 6, 5, 4, 5, 6, 6, 6, 7, 8, 7, 6, 6, 6, 5, 4, 4, 5, 5, 4, 5, 6, 6, 5, 4, 3, 3, 2, 2, 1, 2, 2, 3, 3, 2, 3, 4, 3, 2, 3, 3, 4, 4, 3, 4, 3, 3, 4, 3, 3, 3, 4, 4, 5,...

Q.5 (*) A queue is observed over 10000 one-second time intervals with data as given below in the array odata Construct a Poisson nearest neighbour model with a single arrival and servicing pattern...

U.S. Copyright Law (title 17 of U.S. code) governs the reproduction and redistribution of copyrighted material. Downloading this document for the purpose of redistribution is prohibited. Chapter 15...

Exercises Chapter 2 2.1 Marginal and conditional probability: The social mobility data from Section 2.5 gives a joint probability distribution on (Y1 , Y2 )= (father's occupation, son's occupation)....

Abstract In this paper, the analysis will reveal a significant correlation between body weight and brain weight in various, different mammals. Introduction Talk about your other resources here. What...

Please help me make an Executive Summary. Explain what you will examine in the case study. Write an overview of the field you are researching. Make a thesis statement and sum up the results of your...

In Figure the block has a mass of 1.50 kg and the spring constant is 8.00 N/m. The damping force is given by b(dx/dt), where b = 230 g/s. The block is pulled down 12.0 cm and released. (a) Calculate...

What is the firms current stock price?

Question 4 A company is considering the seven independent investment projects listed below. Each project has an initial investment required, the payoff as a net present value and the time required on...

Kane, CPA, is auditing Star Wholesaling Company's financial statements and is about to perform substantive audit procedures on Star's trade account payable balances. After obtaining an understanding...

What different ways in which supply chains may choose to compete in the marketplace

2 What do you think are the main logistics challenges in running the Tesco operation? Tesco is the UKs largest food retailer, with a sales turnover of more than 67.5 billion. While it has some 638...

What is digital literacy? Why is it necessary?