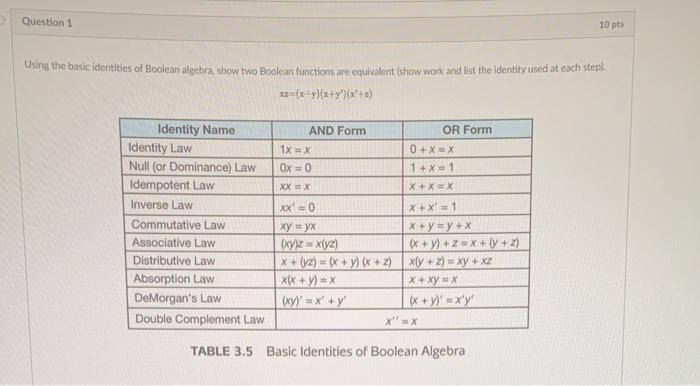
Question 1 10 pts Using the basic identities of Boolean algebra, show two Boolean functions are equivalent (show work and list the identity used at each step). =(x-7)(x+y)(x+) Identity Name Identity Law Null (or Dominance) Law Idempotent Law Inverse Law Commutative Law Associative Law Distributive Law Absorption Law DeMorgan's Law Double Complement Law AND Form OR Form 1x X O + X = X 0x = 0 1+x=1 XX = X X + X X xx'=0 x + x = 1 x + y = y + x (xy}z= xy) (x+y)+2=X+V+z) X+ (y) = (x+y)+2) Xly 2) = XY + XZ x(x + y) = x x + xy + x (XY)' = x + y (x + y) = xy TABLE 3.5 Basic Identities of Boolean Algebra