Question: Question 1. (100 points) Consider a queueing system with two paralel servers and a single waiting line: customers join a single line if both servers

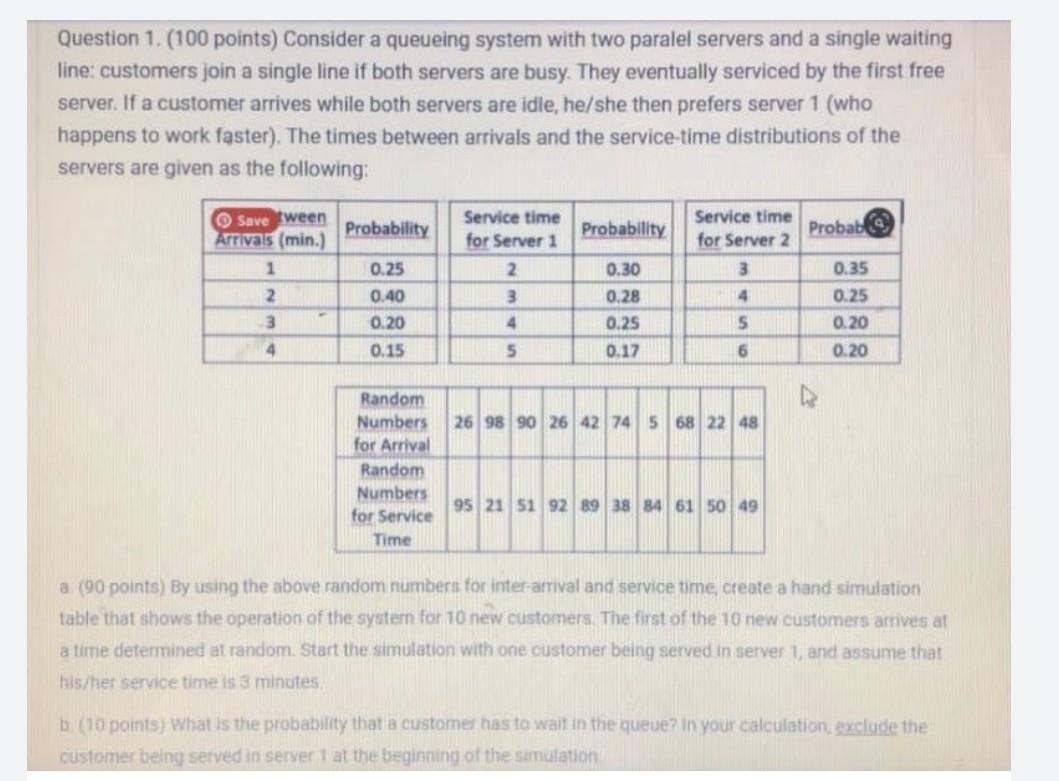
Question 1. (100 points) Consider a queueing

Question 1. (100 points) Consider a queueing system with two paralel servers and a single waiting line: customers join a single line if both servers are busy. They eventually serviced by the first free server. If a customer arrives while both servers are idle, he/she then prefers server 1 (who happens to work faster), The times between arrivals and the service-time distributions of the servers are given as the following: Probability Service time for Server 1 Probability Save tween Arrivals (min.) 1 Service time for Server 2 Probab 2 0.25 0.40 0.20 nmn 0.30 0.28 0.25 0.17 aw 0.35 0.25 0.20 0.20 3 4 0.15 6 26 98 90 26 42 74 5 68 22 48 Random Numbers for Arrival Random Numbers for Service Time 95 21 51 92 89 38 84 61 50 49 8 (90 points) By using the above random numbers for inter arrival and service time create a hand simulation table that shows the operation of the system for 10 new customers The first of the 10 new customers arrives at a time determined at random. Start the simulation with one customer being served in server 1, and assume that his/her service time is 3 minutes b. (10 points) What is the probability that a customer has to wait in the queue? in your calculation exclude the customer being served in server I at the beginning of the simulation

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related General Management Questions!

There are two parallel servers and a single waiting line. Customers are eventually serviced by the first free server. If a customer arrives while both servers are idle, she/he then prefers server 1...

Need it in C++ TITLE QUEUEING SIMULATION INTRODUCTION A queue is a sequence of elements, all of the same type, to which elements can be appended at one end (the rear of the queue) and from which...

TITLE QUEUEING SIMULATION INTRODUCTION A queue is a sequence of elements, all of the same type, to which elements can be appended at one end (the rear of the queue) and from which elements can be...

C++ Project 6 TITLE QUEUEING SIMULATION INTRODUCTION A queue is a sequence of elements, all of the same type, to which elements can be appended at one end (the rear of the queue) and from which...

TITLE QUEUEING SIMULATION INTRODUCTION A queue is a sequence of elements, all of the same type, to which elements can be appended at one end (the rear of the queue) and from which elements can be...

TITLE : C++ QUEUEING SIMULATION INTRODUCTION A queue is a sequence of elements, all of the same type, to which elements can be appended at one end (the rear of the queue) and from which elements can...

TITLE QUEUEING SIMULATION INTRODUCTION A queue is a sequence of elements, all of the same type, to which elements can be appended at one end (the rear of the queue) and from which elements can be...

Under the circumstances in Exercise 20, find the probability of no mutation in a piece of DNA ten thousand codons long. The normal approximation cannot be used in the above case. Why not? Find...

After reading the article, A SWOT Analysis for B2C E-Commerce: The Case of Amazon.com, answer the following question: Should Amazon have remained an online bookstore? Critically evaluate the...

Stock valuation ka marks 4 0 minures Firm \ ( X \ ) projects its growth rate as \ ( 2 0 \ % \ ) per year for the next four yems Ateriour years the sustainable growth rate will fall to \ ( 5 \ % \ )...

Determine the major differences between U.S. GAAP and IFRS disclosure reporting requirements related to each separately reportable operating segment. Next, give your opinion as to whether either U.S....