Question 1:(15 points)

In the content-based recommender system, suppose that we have the following user profile:

User ID	Square	Circle	Hexagon	Triangle	Red	Green	Blue
u1

0.75

0.5

0.75

0.5

0.25

0.5

1

Suppose that we have the following new items:

Item ID	Square	Circle	Hexagon	Triangle	Red	Green	Blue
t1

	0	0	1	0	1	0	0
t2

	0	1	0	0	0	1	0
t3

	1	0	0	0	0	0	1
t4

1

0

0

0

0

1

0

Using the cosine similarity: cos(a,b)=?a,b?/(?a???b?)

, which item does the recommender system recommend?

Question 2:(15 points)

In the matrix factorization, suppose that there are three users u1,u2,u3

and four items t1,t2,t4,t4

, and their representation in the two-dimensional latent space are

???0.20.30.70.50.50.8???

and

?????1.23.10.32.52.41.54.40.4?????

What is the prediction of the interaction between user u2 and t3

?

Question 3:(20 points)

The following are the seasonal indices by the classical multiplicative decomposition method:

Month	Seasonal Indices
Jan	76.96
Feb	71.27
Mar	77.91
Apr	91.34
May	104.83
Jun	116.09
Jul	116.76
Aug	122.94
Sep	123.55
Oct	119.28
Nov	99.53
Dec	83.59

Assuming the trend in the data is Tt=894.11+8.85t

, where t=1 is January of year 1 and t=60

is December of year 5, show forecasts for the 12 months of year 6. (Hint: divide the seasonal indices by 100 to get the seasonal multiplicative ratio)

Question 4:(30 points)

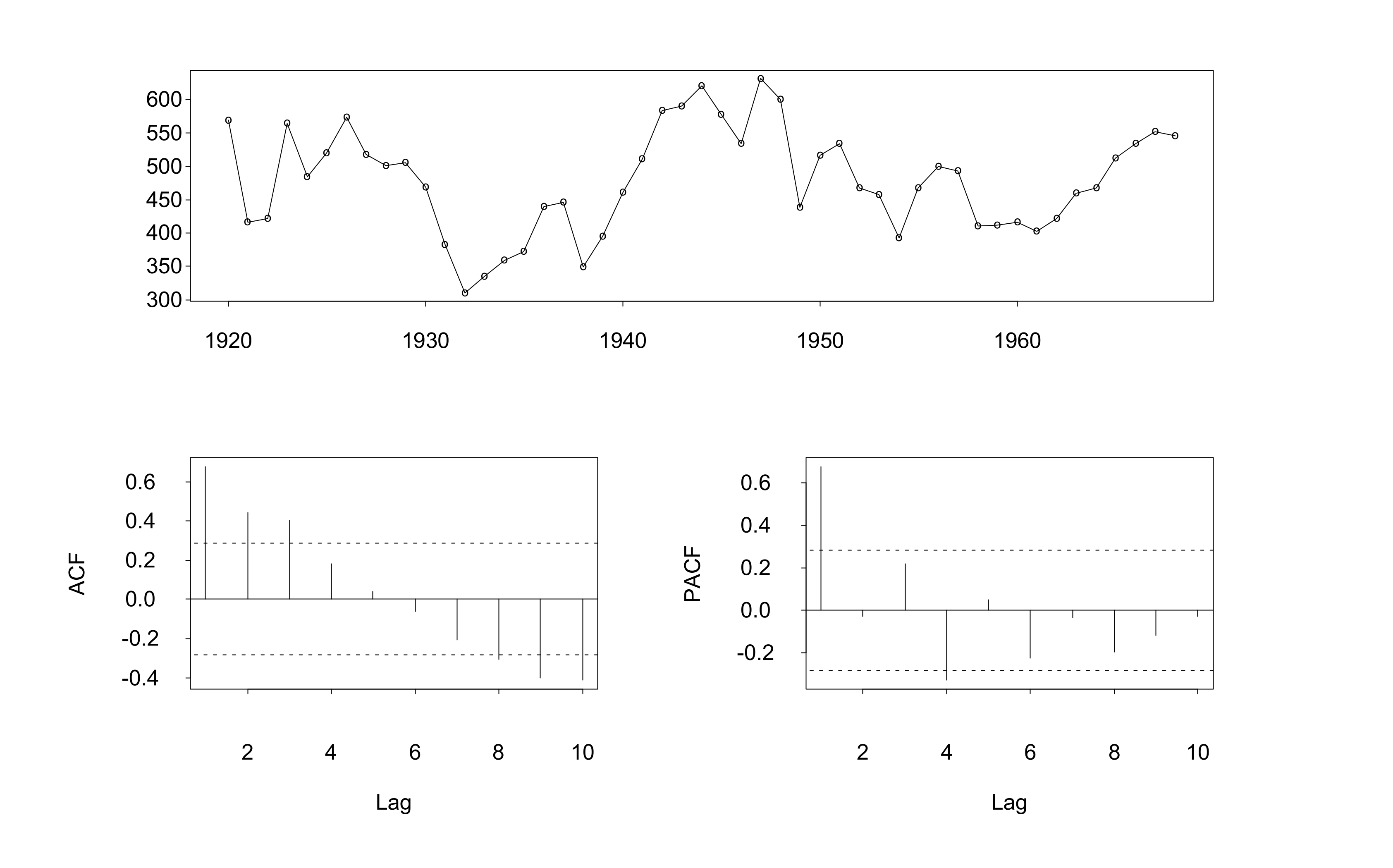
The following figure shows the annual bituminous coal production in the United States from 1920 to 1968. Suppose that you decide to fit the following model to the series:

Yt=c+?1Yt?1+?2Yt?2+?3Yt?3+?4Yt?4+et

where Yt

is the coal production in year t and et

is a white noise series.

\f