Question: Question 1 (20 points) Let f(x) = 0 if x is any rational number and f(x) = 1 if x is any irrational number. Show
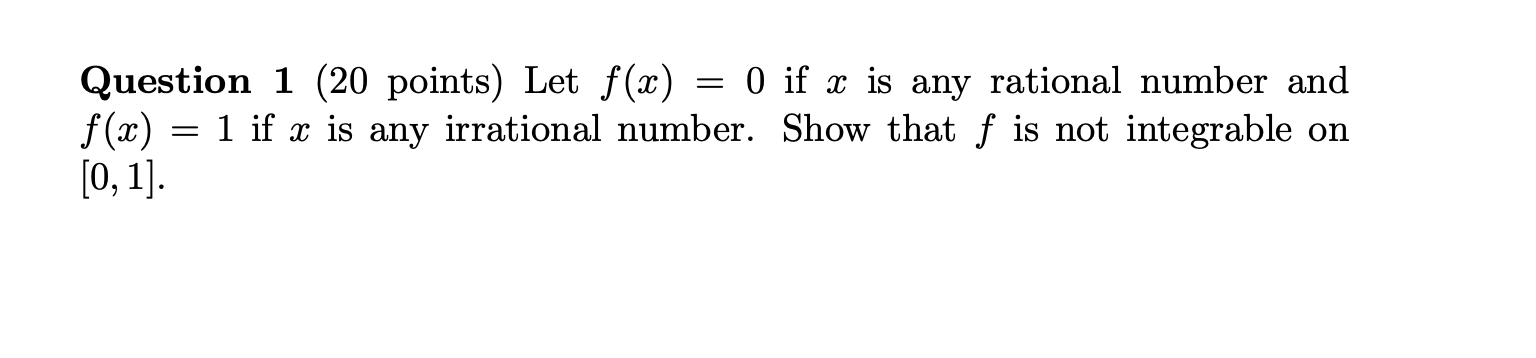
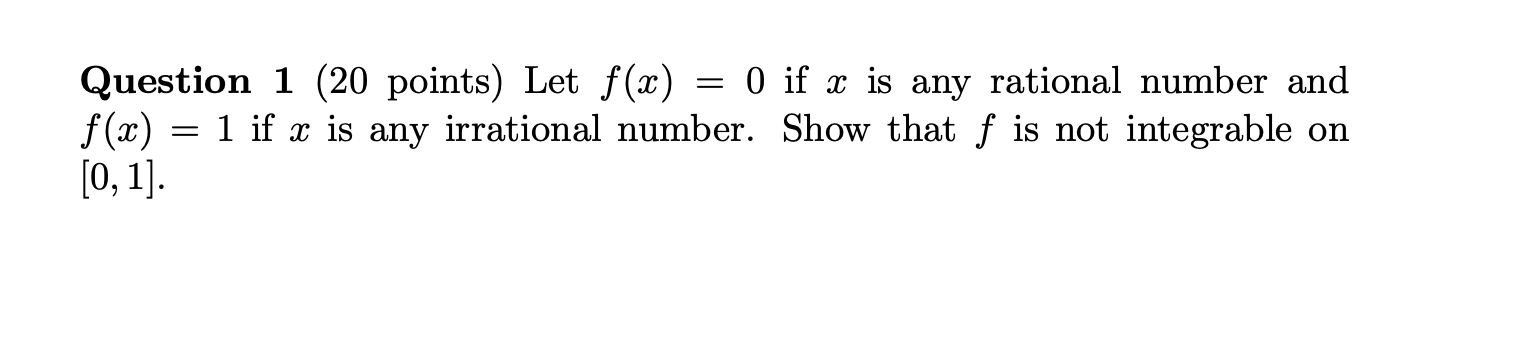
![number. Show that f is not integrable on [0, 1].Question 1 (20](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/10/67095a2649f89_15067095a2631527.jpg)
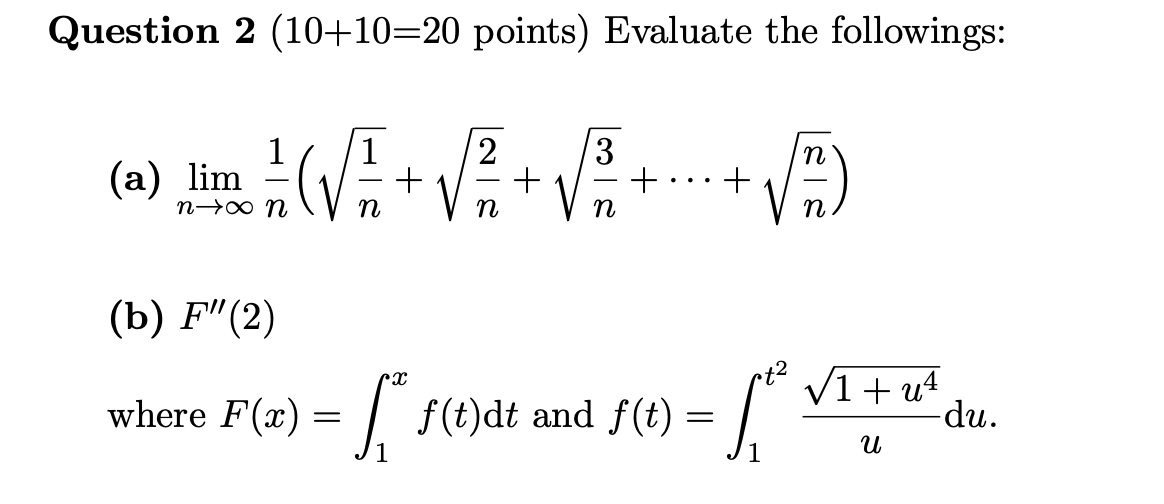
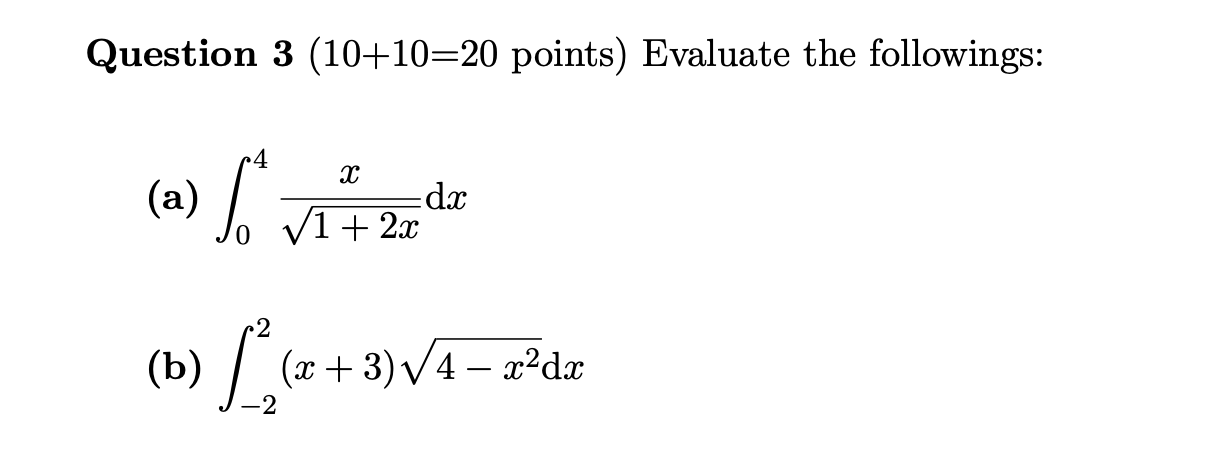
![is not integrable on [0, 1].Question 2 (10+10=20 points) Evaluate the followings:](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/10/67095a271a775_15167095a27051ae.jpg)
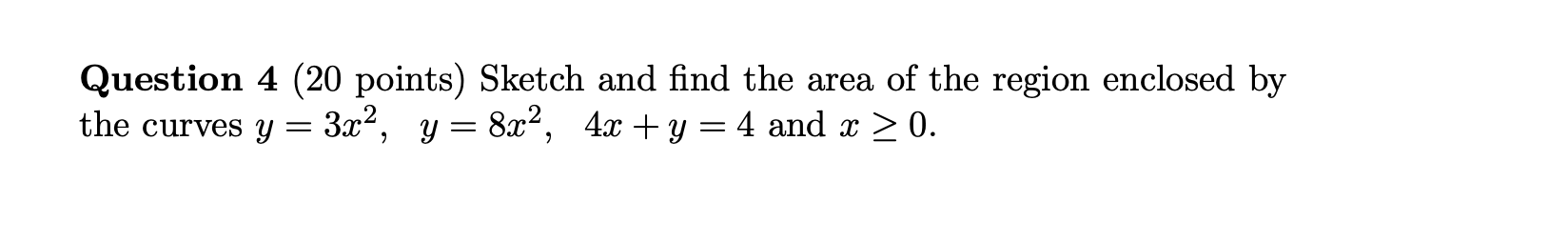
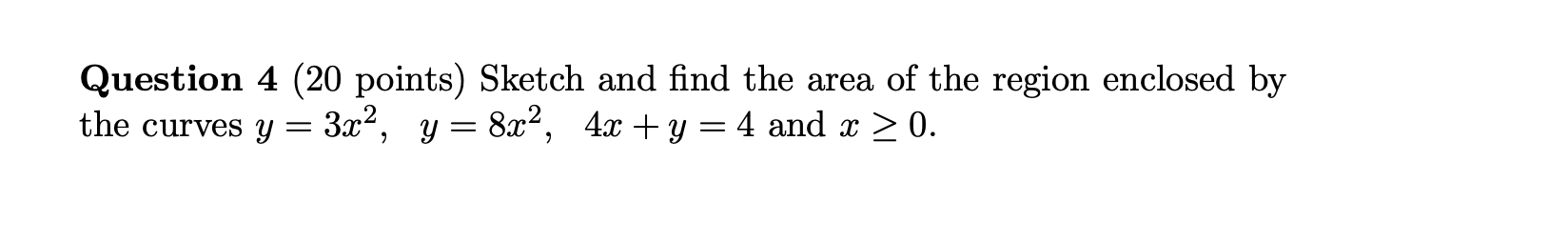


Question 1 (20 points) Let f(x) = 0 if x is any rational number and f(x) = 1 if x is any irrational number. Show that f is not integrable on [0, 1].Question 1 (20 points) Let f(x) = 0 if x is any rational number and f(x) = 1 if x is any irrational number. Show that f is not integrable on [0, 1].Question 2 (10+10=20 points) Evaluate the followings: N n (a) lim + + 3 1 00 + . . + n-toon n (b) F"(2) +2 V1 + u where F(x) = f (t) dt and f (t) = du. uQuestion 2 (10+10=20 points) Evaluate the followings: N n (a) lim + + 3 1 00 + . . + n-toon n (b) F"(2) +2 V1 + u where F(x) = f (t) dt and f (t) = du. u\f\fQuestion 4 (20 points) Sketch and find the area of the region enclosed by the curves y = 322, y=8z2, 4r+y=4and z > 0. Question 4 (20 points) Sketch and find the area of the region enclosed by the curves y = 322, y=8z2, 4r+y=4and z > 0. Question 5 (14+6=20 points) Let f be a one-to-one, twice differentiable function with inverse function g. (a) Show that M) f"(g9(z)) S = (lg)P (b) Deduce that if f is increasing and concave upward, then its inverse function is concave downward. Question 5 (14+6=20 points) Let f be a one-to-one, twice differentiable function with inverse function g. (a) Show that M) f"(g9(z)) S = (lg)P (b) Deduce that if f is increasing and concave upward, then its inverse function is concave downward
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


