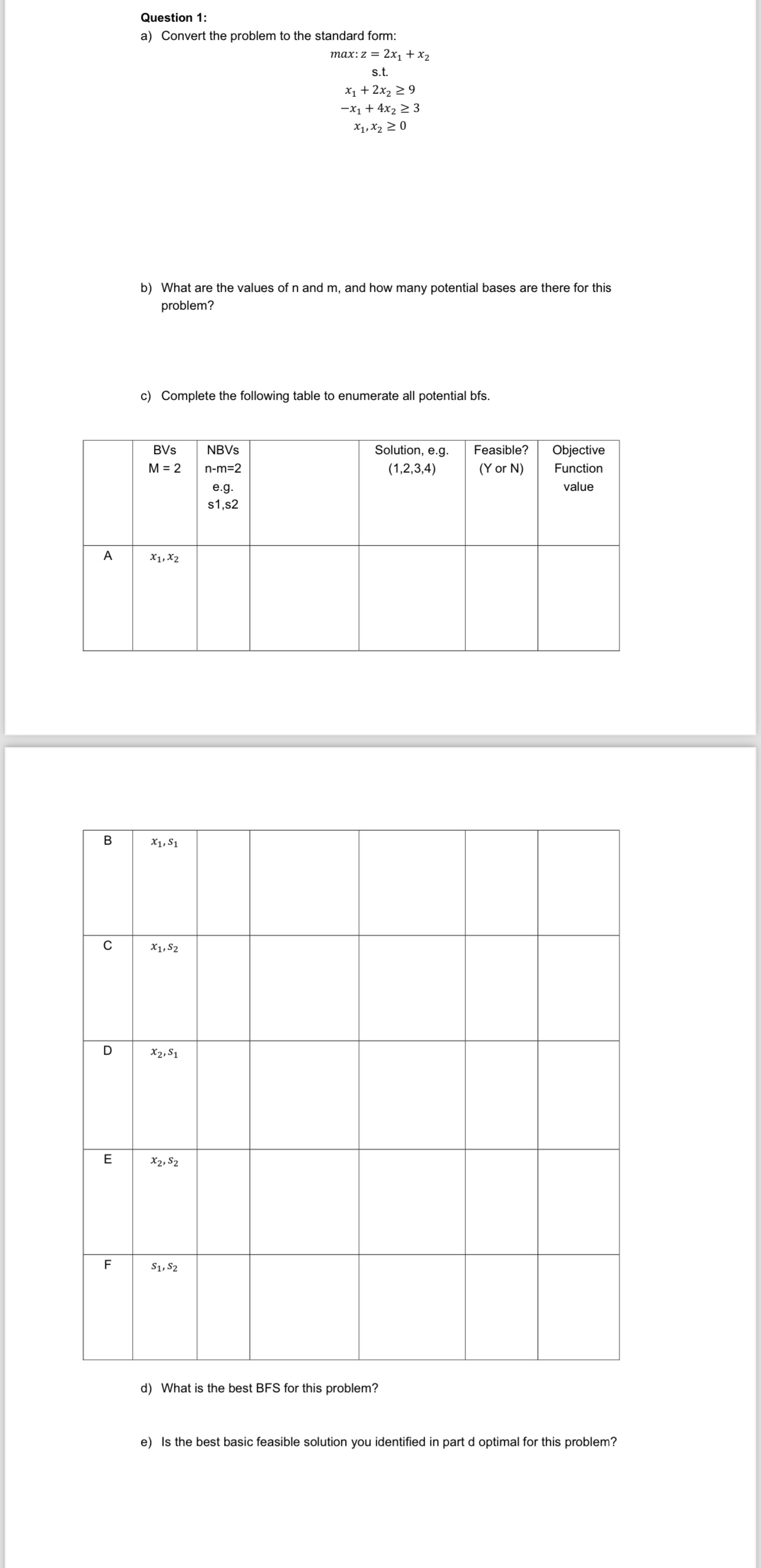
Question $1$:

a$)$ Convert the problem to the standard form:

max:$z=2x_1+x_2$

$s.t.$

$x_1+2x_{2}9$

$-x_1+4x_{2}3$

$x_1,x_{2}0$

b$)$ What are the values of $n$ and $m,$ and how many potential bases are there for this problem?

c$)$ Complete the following table to enumerate all potential bfs$.$

$\backslash$table$[[,$BVs$,$NBVs$,,,,],[$M$=2,\backslash$table$[[$n$-$m$=2],[$e$.$g$.],[$s$1,$s$2]],,$Solution, e$.$g$.,$Feasible?,Objective,$],[($Y or N$),\backslash$table$[[$Function$],[$value$]],,,,,],[$A$,x_1,x_2,,,,,],[,,,,,,]]$

d$)$ What is the best BFS for this problem?

e$)$ Is the best basic feasible solution you identified in part d optimal for this problem?