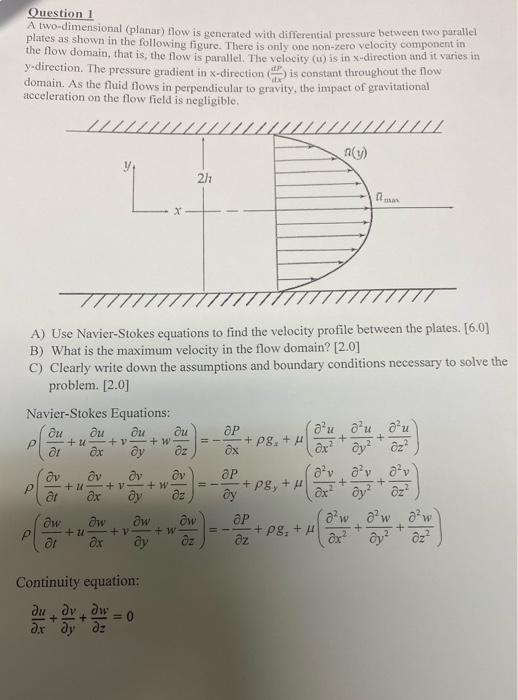
Question 1 A two-dimensional (planar) flow is generated with differential pressure between two parallel plates as shown in the following figure. There is only one non-zero velocity component in the flow domain, that is, the flow is parallel. The velocity (u) is in x-direction and it varies in y-direction. The pressure gradient in x-direction (dxdP) is constant throughout the flow domain. As the fluid flows in perpendicular to gravity, the impact of gravitational acceleration on the flow field is negligible. A) Use Navier-Stokes equations to find the velocity profile between the plates. [6.0] B) What is the maximum velocity in the flow domain? [2.0] C) Clearly write down the assumptions and boundary conditions necessary to solve the problem. [2.0] Navier-Stokes Equations: Navier-StokesEquations:(tu+uxu+vyu+wzu)=xP+gx+(x22u+y22u+z22u)(tv+uxv+vyv+wzv)=yP+gy+(x22v+y22v+z22v)(tw+uxw+vyw+wzw)=zP+gx+(x22w+y22w+z22w) Continuity equation: xu+yv+zw=0