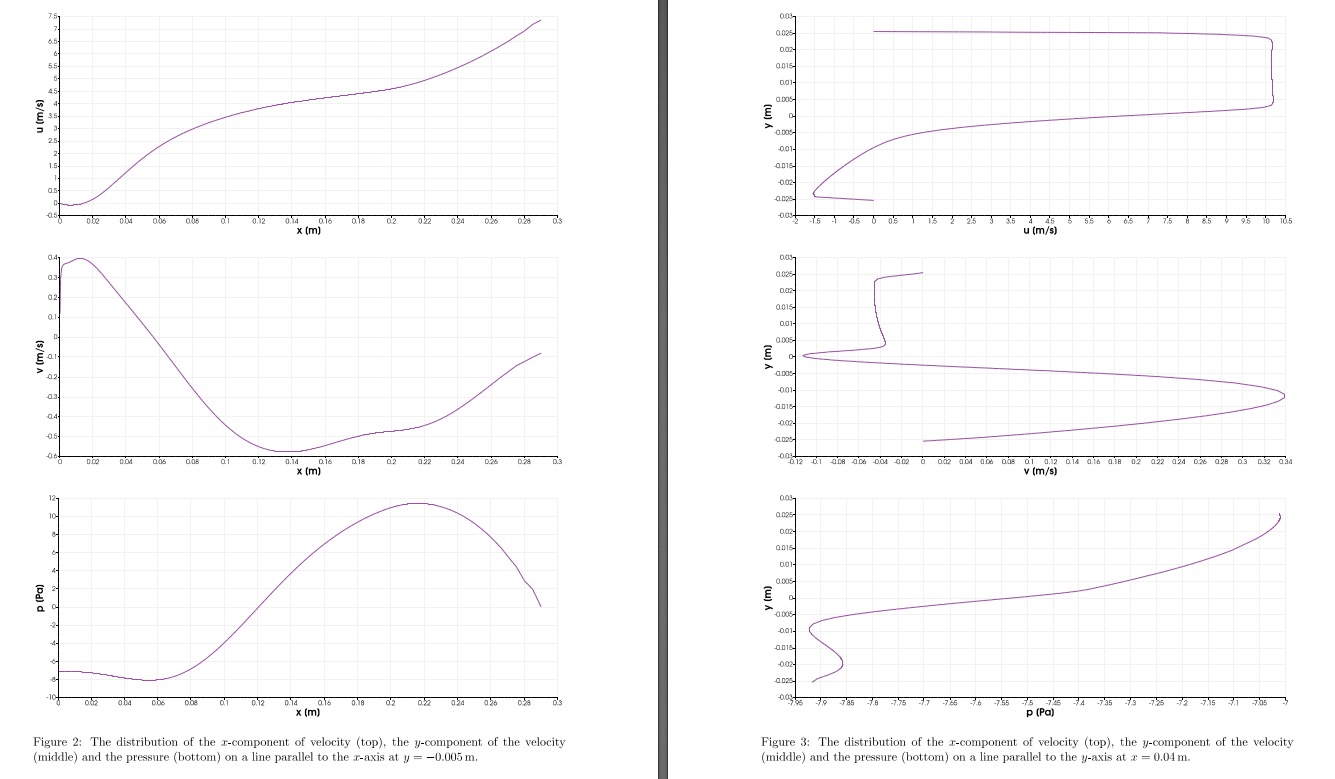
MEC$-$E$1020$ Fluid dynamics $-$ Week $1-$ DL $28\mathrm{.}10.$ at $14$:$15$ The purpose of the exercise is to get you familiar with the notations, with the physical meaning of the various terms in the fundamental flow equations and the link between the different terms. By studying the terms in a particular flow case and relating the terms to the details of the flow field, you can concretely see, what kind of balances there are between different physical processes. Task statement $1.$ Open up the following terms into the full component form$\mathrm{.}1$ The equation numbers refer to Kundu and Cohen. $($a$)$ The vector components of the stress on a surface with normal in the positive z$-$direction based on the constitutive equation $(4\mathrm{.}41).$ Open up the strain rate tensor eij in terms of the velocity components. Identify the normal and tangential components of the stress on this surface. $($b$)$ The rate of work by surface force Z A uiijdAj $.(1)$ Do not use a constitutive relation, i$.$e$.$ write the rate of work using the components of the stress tensor. $2.$ Consider the two$-$dimensional, incompressible Pitz$-$Daily flow over a backward facing step that was discussed in the description session. Let$$s study the conservation of mass and balance of momentum for a rectangular differential fluid particle at point $($x$,$ y$)=(0\mathrm{.}04$ m$,0\mathrm{.}005$ m$).$ Assume that the faces of the differential fluid element are perpendicular to the coordinate axes. The influence of gravity is neglected. The global flow field in terms of the velocity components and the pressure are shown in Fig. $1.$ The distributions of the velocity components and the pressure along two lines parallel to the x$-$ and y$-$axes and passing through the point of interest are shown in Figs. $2$ and $3$ respectively. Support your claims in all of the points below by relevant analysis of the distributions. The analysis does not have to be very exact in terms of numbers but sufficiently accurate to justify your claims. Points will be awarded only for claims that have been supported by analysis. $($a$)$ Is mass conserved at the point of interest? How does the conservation of mass show in the deformation of the differential fluid element of interest? $(0\mathrm{.}5$p$)($b$)$ Specify the direction of the flow at the point of interest. What can you say about the signs of the components of the acceleration of the differential fluid particle? $(0\mathrm{.}5$p$)($c$)$ Specify the signs of the components of the net pressure and viscous force acting on the differential fluid particle at the point of interest. Do these make sense from the point of view of subtask b$?(1$p$)3.$ Consider steady, incompressible, fully developed flow in a horizontal straight pipe section. The control volume is the fluid filling this whole pipe section with the surface of the control volume consisting of three parts: the upstream cross$-$section, the downstream cross$-$section, and the pipe wall. Assume that the pipe walls are insulated and thus, heat transfer can be neglected. $($a$)$ Discuss the contributions of the work by surface forces on the different parts of the control volume surface as well as the sum of these contributions, i$.$e$.$ the term in task $1$b$.$ You do not need to evaluate the term, but discuss whether the contributions on the different surfaces are positive, negative or zero, and which stresses $($tangential$,$ normal, pressure, viscous$)$ contribute to the work. $(0\mathrm{.}5$p$)1$Full component form here means that, if you have e$.$g$.$ a term a $$ b $=$ aibi, where a and b are vectors, the full component form is a$1$b$1+$ a$2$b$2+$ a$3$b$3.1$ Figure $1$: The distribution of the x$-$component of velocity $($top$),$ the y$-$component of the velocity $($middle$)$ and the pressure $($bottom$).2$ Figure $2$: The distribution of the x$-$component of velocity $($top$),$ the y$-$component of the velocity $($middle$)$ and the pressure $($bottom$)$ on a line parallel to the x$-$axis at y $=0\mathrm{.}005$ m$.3$ Figure $3$: The distribution of the x$-$component of velocity $($top$),$ the y$-$component of the velocity $($middle$)$ and the pressure $($bottom$)$ on a line parallel to the y$-$axis at x $=0\mathrm{.}04$ m$.4($b$)$ Discuss the conservation of energy in terms of Eqs. $(4\mathrm{.}63)$ and $(4\mathrm{.}64)$ for the fluid in the pipe section and specifically how the different terms of the equation balance each other. Hints and advice Here is some hopefully useful additional info to get you started with the assignments. The numbers in the list refer to the subtasks. $1.$ The idea here is to practice the index or indical notation used often in the equations. The notations used in the equations typically aim for compact notation, which makes it easier to focus on the relevant physics. The large number of terms and the associated clutter in the full form makes this more difficult. However, the actual evaluation of the terms often requires that the terms are opened up into their full form and this should, thus, be practiced. $($a$)$ This is supposed to be a straightforward task. The first thing to figure out is$,$ how the indices in Eq$.(4\mathrm{.}41)$ relate to the information given in the task statement. The stress ten Figu